Missing Values, Categorical Features, and Text

In this notebook, we discuss:

  1. how to deal with missing values
  2. how to encode categorical features,
  3. and how to encode text features.

In the process, we will work through feature engineering to construct a model that predicts vehicle efficiency.

The Data

For this notebook, we will use the seaborn mpg data set which describes the fuel mileage (measured in miles per gallon or mpg) of various cars along with characteristics of those cars. Our goal will be to build a model that can predict the fuel mileage of a car based on the characteristics of that car.

Quantitative Continuous Features

This data set has several quantitative continuous features that we can use to build our first model. However, even for quantitative continuous features, we may want to do some additional feature engineering. Things to consider are:

  1. transforming features with non-linear functions (log, exp, sine, polynomials)
  2. constructing products or ratios of features
  3. dealing with missing values

Missing Values

We can use the Pandas DataFrame.isna function to find rows with missing values:

There are many ways to deal with missing values. A common strategy is to substitute the mean. Because missing values can actually be useful signal, it is often a good idea to include a feature indicating that the value was missing.

Using our feature function, we can fit our first model to the transformed data:

Keeping Track of Progress

Because we are going to be building multiple models with different feature functions it is important to have a standard way to track each of the models.

The following function takes a model prediction function, the name of a model, and the dictionary of models that we have already constructed. It then evaluates the new model on the data and plots how the new model performs relative to the previous models as well as the $Y$ vs $\hat{Y}$ scatter plot.

In addition, it updates the dictionary of models to include the new model for future plotting.

Stable Feature Functions

Unfortunately, the feature function we just implemented applies a different transformation depending on what input we provide. Specifically, if the horesepower is missing when we go to make a prediction we will substitute it with a different mean then was used when we fit our model. Furthermore, if we only want predictions on a few records and the horsepower is missing from those records then the feature function will be unable to substitute a meaningful value.

For example, if we were to get new records that look like the following:

The feature function is be unable to substitute the mean since none of the records have a horsepower value.

We can fix this by computing the mean on the original data and using that mean on any new data.

Scikit-learn Model Imputer

Because these kinds of transformations are fairly common. Scikit-learn has built-in transformations for data imputation. These transformations have a common pattern of fit and transform. You first fit the transformation to your data and then you can transform your data and any future data using the same transformation.

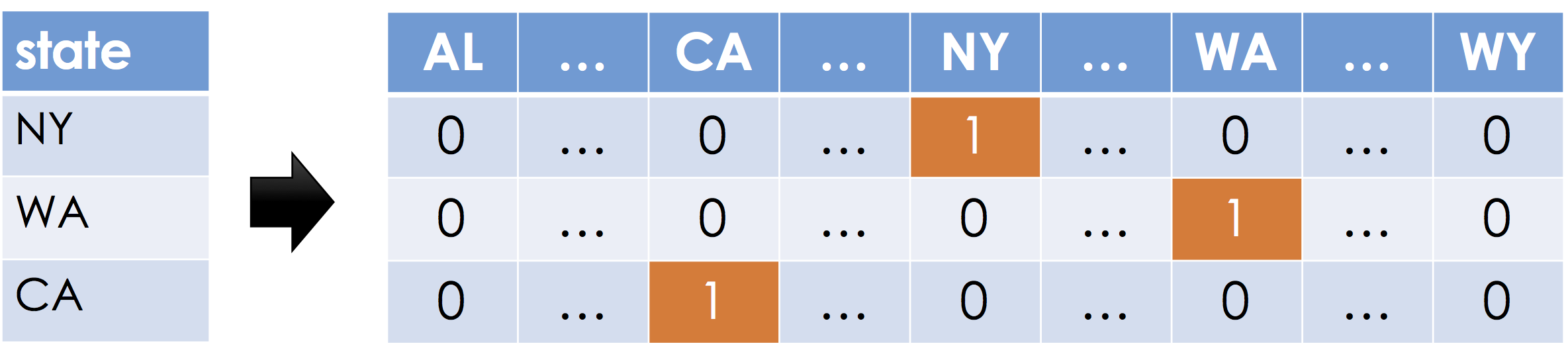
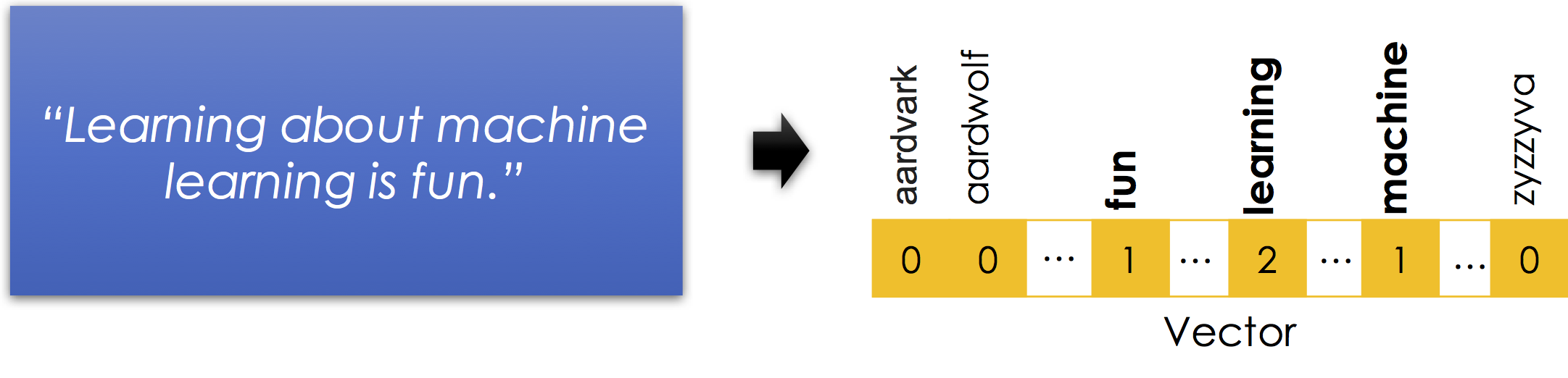
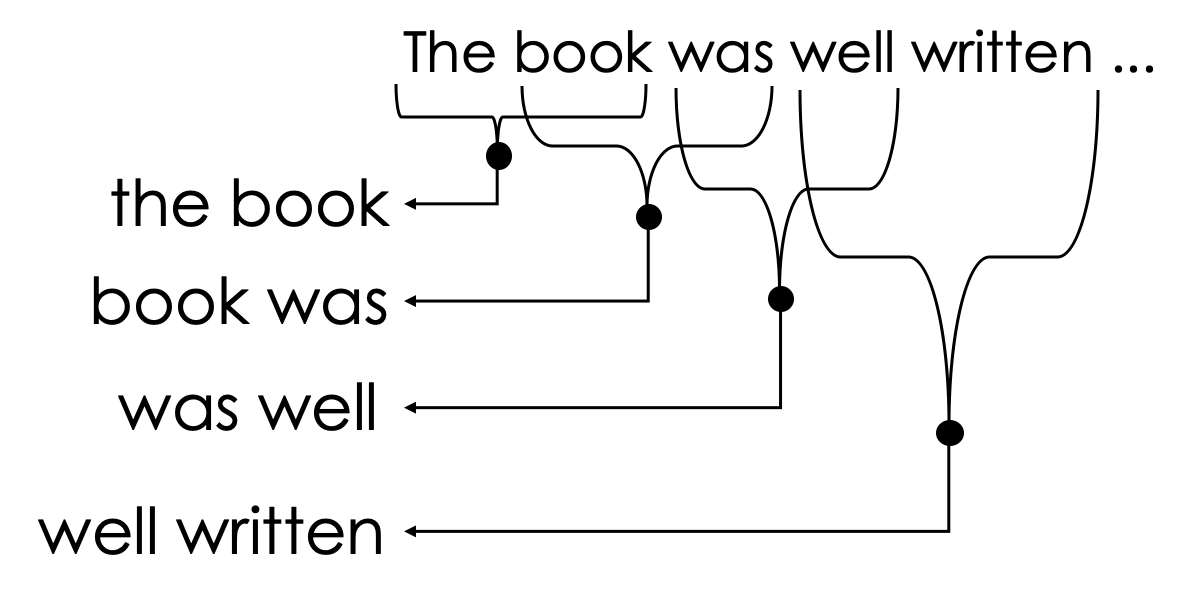
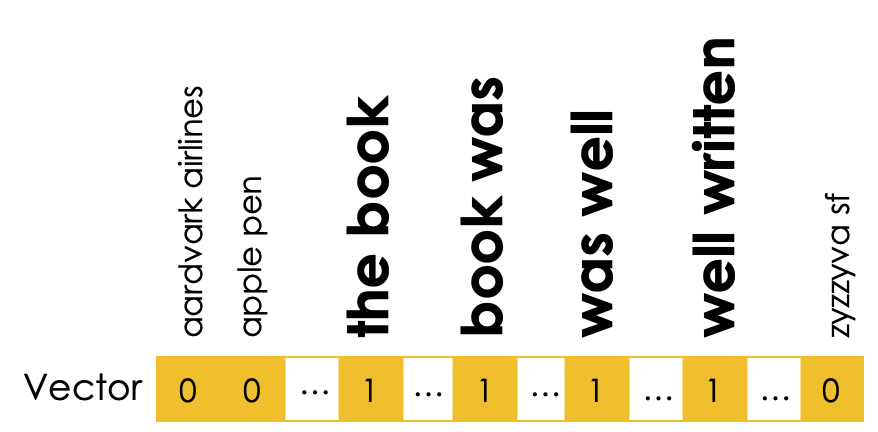
Applying Domain Knowledge

The displacement of an engine is defined as the product of the volume of each cylinder and number of cylinders. However, not all cylinders fire at the same time (at least in a functioning engine) so the fuel economy might be more closely related to the volume of any one cylinder.

Cylinders from https://gifimage.net/piston-gif-3/

We can use this "domain knowledge" to compute a new feature encoding the volume per cylinder by taking the ratio of displacement and cylinders.

Again fitting and evaluating our model we see a reduction in prediction error (RMSE).

Encoding Categorical Data

The origin column in this data set is categorical (nominal) data taking on a fixed set of possible values.

To use this kind of data in a model, we need to transform into a vector encoding that treats each distinct value as a separate dimension. This is called One-hot Encoding or Dummy Encoding.

One-Hot Encoding (Dummy Encoding)

One-Hot encoding, sometimes also called dummy encoding is a simple mechanism to encode categorical data as real numbers such that the magnitude of each dimension is meaningful. Suppose a feature can take on $k$ distinct values (e.g., $k=50$ for 50 states in the United Stated). A new feature (dimension) is created for each distinct value. For each record, all the new features are set to zero except the one corresponding to the value in the original feature.

The term one-hot encoding comes from a digital circuit encoding of a categorical state as particular "hot" wire:

Dummy Encoding in Pandas

We can construct a one-hot (dummy) encoding of the origin column using the Pandas.get_dummies function:

Using the Pandas.get_dummies, we can build a new feature function which extends our previous features with the additional dummy encoding columns.

We fit a new model with the origin feature encoding:

Unfortunately, the above feature function is not stable. For example, if we are given a single vehicle to make a prediction the model will fail:

To see why this fails look at the feature transformation for a single row:

The dummy columns are not created for the other categories.

There are a couple solutions. We could maintain a list of dummy columns and always add these columns. Alternatively, we could use a library function designed to solve this problem. The second option is much easier.

Scikit-learn One-hot Encoder

The scikit-learn library has a wide range feature transformations and a framework for composing them in reusable (stable) pipelines. Let's first look at a basic OneHotEncoder transformation.

We then fit that instance to some data. This is where we would determine the specific values that a categorical feature can take:

Once we fit the transformation, we can then use it transform new data:

We can also inspect the categories of the one-hot encoder:

We can update our feature function to use the one-hot encoder instead.

Encoding Text Features

The only remaining feature to encode is the vehicle name. Is there potentially signal in the vehicle name?

Encoding text can be challenging. The capturing the semantics and grammar of language in mathematical (vector) representations is an active area of research. State-of-the-art techniques often rely on neural networks trained on large collections of text. In this class, we will focus on basic text encoding techniques that are still widely used. If you are interested in learning more, checkout BERT Explained: A Complete Guide with Theory and Tutorial.

Here we present two widely used representations of text:

Both of these encoding strategies are related to the one-hot encoding with dummy features created for every word or sequence of words and with multiple dummy features having counts greater than zero.

The Bag-of-Words Encoding

The bag-of-words encoding is widely used and a standard representation for text in many of the popular text clustering algorithms. The following is a simple illustration of the bag-of-words encoding:

Notice

  1. Stop words are often removed. Stop-words are words like is and about that in isolation contain very little information about the meaning of the sentence. Here is a good list of stop-words in many languages.
  2. Word order information is lost. Nonetheless the vector still suggests that the sentence is about fun, machines, and learning. Thought there are many possible meanings learning machines have fun learning or learning about machines is fun learning ...
  3. Capitalization and punctuation are typically removed. However, emoji symbols may be worth preserving.
  4. Sparse Encoding: is necessary to represent the bag-of-words efficiently. There are millions of possible words (including terminology, names, and misspellings) and so instantiating a 0 for every word that is not in each record would be inefficient.

Professor Gonzalez is an "artist"

When professor Gonzalez was a graduate student at Carnegie Mellon University, he and several other computer scientists created the following art piece on display in the Gates Center:

Is this art or science?

Notice

  1. The unordered collection of words in the bag.
  2. The stop words on the floor.
  3. The missing broom. The original sculpture had a broom attached but the janitor got confused ....

Bag-of-words in Scikit-learn

We can use scikit-learn to construct a bag-of-words representation of text

The N-Gram Encoding

The n-gram encoding is a generalization of the bag-of-words encoding designed to capture information about word ordering. Consider the following passage of text:

The book was not well written but I did enjoy it.

If we re-arrange the words we can also write:

The book was well written but I did not enjoy it.

Moreover, local word order can be important when making decisions about text. The n-gram encoding captures local word order by defining counts over sliding windows. In the following example a bi-gram ($n=2$) encoding is constructed:

The above n-gram would be encoded in the sparse vector:

Notice that the n-gram captures key pieces of sentiment information: "well written" and "not enjoy".

N-grams are often used for other types of sequence data beyond text. For example, n-grams can be used to encode genomic data, protein sequences, and click logs.

N-Gram Issues

  1. Maintaining the dictionary of possible n-grams can be very costly. There are several approximations leveraging hashing that can be used to closely approximate n-gram encoding without the need to maintain the dictionary of all possible n-grams.
  2. As the size $n$ of n-grams increases the chance of observing more than one instance decreases limiting their value as a feature.

Applying Text Encoding

We can add the text encoding features to our feature function:

Quick Reflection

Notice that as we added more features we were able to improve the accuracy of our model. This is not always a good thing and we will see the problems associated with this in a future lecture.

It is also worth noting that our feature functions each depended on the last and the in some cases we were converting sparse features to dense features. There is a better way to deal with feature pipelines using the scikit-learn pipelines module.

Success!!!!!