Diversity and Data Science:¶
Unfortunately, surveys of data scientists suggest that there are far fewer women in data science:
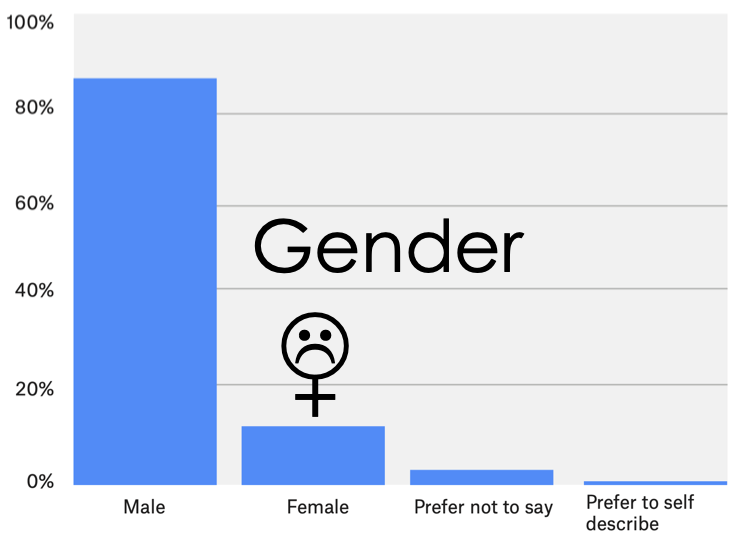
To learn more checkout the Kaggle Executive Summary or study the Raw Data.
by Joseph E. Gonzalez
adapted from Anthony D. Joseph, Josh Hug, Suraj Rampure
import pandas as pd
import numpy as np
## Plotly plotting support
import plotly.offline as py
py.init_notebook_mode()
import plotly.graph_objs as go
import plotly.figure_factory as ff
import plotly.express as px
names = pd.read_csv("data/names.csv")
majors = pd.read_csv("data/majors.csv")
names.head()
| Name | |
|---|---|
| 0 | Andrew |
| 1 | Justin |
| 2 | Michael |
| 3 | JUSTIN |
| 4 | Michael |
names["Name"] = names["Name"].str.lower()
names.head()
| Name | |
|---|---|
| 0 | andrew |
| 1 | justin |
| 2 | michael |
| 3 | justin |
| 4 | michael |
majors.head(20)
| Majors | Terms in Attendance | |
|---|---|---|
| 0 | Economics BA | 8 |
| 1 | Letters & Sci Undeclared UG | 6 |
| 2 | Industrial Eng & Ops Rsch MEng | G |
| 3 | Letters & Sci Undeclared UG | 6 |
| 4 | Mechanical Engineering BS | 4 |
| 5 | Industrial Eng & Ops Rsch BS | 6 |
| 6 | Letters & Sci Undeclared UG | 4 |
| 7 | Economics BA | 8 |
| 8 | Molecular & Cell Biology BA | 6 |
| 9 | Data Science BA | 6 |
| 10 | MCB-Biochem & Mol Biol BA | 8 |
| 11 | Political Science BA | 4 |
| 12 | Letters & Sci Undeclared UG | 6 |
| 13 | Computer Science BA, Public Health BA | 8 |
| 14 | Computer Science BA | 6 |
| 15 | Chemical Engineering BS | 6 |
| 16 | Economics BA | 6 |
| 17 | Letters & Sci Undeclared UG | 7 |
| 18 | Letters & Sci Undeclared UG | 4 |
| 19 | Electrical Eng & Comp Sci BS | 6 |
names.describe()
| Name | |
|---|---|
| count | 1090 |
| unique | 798 |
| top | michael |
| freq | 13 |
majors.describe()
| Majors | Terms in Attendance | |
|---|---|---|
| count | 1090 | 1090 |
| unique | 162 | 8 |
| top | Letters & Sci Undeclared UG | 4 |
| freq | 305 | 366 |
What are the top majors:
majors["Majors"].value_counts().sort_values().tail(20)
# majors["Majors"].str.split(",").explode().value_counts().sort_values().tail(20)
Business Administration BS, Electrical Eng & Comp Sci BS 8 Public Policy MPP 8 Materials Science & Eng BS 8 Data Science BA, Economics BA 8 Mechanical Engineering BS 8 Environ Econ & Policy BS 9 Chemical Biology BS 9 Public Health BA 10 Industrial Eng & Ops Rsch MEng 10 Chemical Engineering BS 12 Bioengineering BS 14 Molecular & Cell Biology BA 16 Cognitive Science BA 24 Civil Engineering BS 28 Applied Mathematics BA 33 Data Science BA 47 Economics BA 73 Electrical Eng & Comp Sci BS 84 Computer Science BA 121 Letters & Sci Undeclared UG 305 Name: Majors, dtype: int64
fig = px.bar(majors["Majors"].value_counts().sort_values().tail(20),
orientation="h")
fig.update_layout(dict(showlegend=False, xaxis_title="Count", yaxis_title="Major"))
fig = px.bar(majors["Terms in Attendance"].value_counts())
fig.update_layout(xaxis_title="Term", yaxis_title="Count", showlegend=False)
Unfortunately, surveys of data scientists suggest that there are far fewer women in data science:

To learn more checkout the Kaggle Executive Summary or study the Raw Data.
I actually get asked this question a lot as we try to improve the data science program at Berkeley.
This is actually a fairly complex question. What do we mean by female? Is this a question about the sex or gender identity of the students? They are not the same thing.
Most likely, my colleagues are interested in improving gender diversity, by ensuring that our program is inclusive.
print(majors.columns)
print(names.columns)
Index(['Majors', 'Terms in Attendance'], dtype='object') Index(['Name'], dtype='object')
What I am about to do is flawed in so many ways and we will discuss these flaws in a moment and throughout the semester. However, it will illustrate some very basic inferential modeling and how we might combine multiple data sources to try and reason about something we haven't measured.
In Data 100 you will have to learn about different data sources (and their limitations) on your own.
Reading from SSN Office description:
All names are from Social Security card applications for births that occurred in the United States after 1879. Note that many people born before 1937 never applied for a Social Security card, so their names are not included in our data. For others who did apply, our records may not show the place of birth, and again their names are not included in our data.
To safeguard privacy, we exclude from our tabulated lists of names those that would indicate, or would allow the ability to determine, names with fewer than 5 occurrences in any geographic area. If a name has less than 5 occurrences for a year of birth in any state, the sum of the state counts for that year will be less than the national count.
All data are from a 100% sample of our records on Social Security card applications as of March 2020.
import urllib.request
import os.path
# Download data from the web directly
data_url = "https://www.ssa.gov/oact/babynames/names.zip"
local_filename = "babynames.zip"
if not os.path.exists(local_filename): # if the data exists don't download again
with urllib.request.urlopen(data_url) as resp, open(local_filename, 'wb') as f:
f.write(resp.read())
# Load data without unzipping the file
import zipfile
babynames = []
with zipfile.ZipFile(local_filename, "r") as zf:
data_files = [f for f in zf.filelist if f.filename[-3:] == "txt"]
def extract_year_from_filename(fn):
return int(fn[3:7])
for f in data_files:
year = extract_year_from_filename(f.filename)
with zf.open(f) as fp:
df = pd.read_csv(fp, names=["Name", "Sex", "Count"])
df["Year"] = year
babynames.append(df)
babynames = pd.concat(babynames)
babynames.head()
| Name | Sex | Count | Year | |
|---|---|---|---|---|
| 0 | Mary | F | 7065 | 1880 |
| 1 | Anna | F | 2604 | 1880 |
| 2 | Emma | F | 2003 | 1880 |
| 3 | Elizabeth | F | 1939 | 1880 |
| 4 | Minnie | F | 1746 | 1880 |
A little bit of data cleaning:
babynames['Name'] = babynames['Name'].str.lower()
babynames.tail()
| Name | Sex | Count | Year | |
|---|---|---|---|---|
| 31949 | zyheem | M | 5 | 2019 |
| 31950 | zykel | M | 5 | 2019 |
| 31951 | zyking | M | 5 | 2019 |
| 31952 | zyn | M | 5 | 2019 |
| 31953 | zyran | M | 5 | 2019 |
How many people does this data represent?
format(babynames['Count'].sum(), ',d')
'355,149,899'
format(babynames.shape[0], ',d')
'1,989,401'
Trying a simple query:
babynames[(babynames['Name'] == 'nora') & (babynames['Year'] == 2018)]
| Name | Sex | Count | Year | |
|---|---|---|---|---|
| 29 | nora | F | 5831 | 2018 |
| 28504 | nora | M | 7 | 2018 |
Let's use this data to estimate the fraction of female students in the class.
In this example we construct a pivot table which aggregates the number of babies registered for each year by Sex.
year_sex = pd.pivot_table(babynames,
index=['Year'], # the row index
columns=['Sex'], # the column values
values='Count', # the field(s) to processed in each group
aggfunc=np.sum,
)
year_sex.head()
| Sex | F | M |
|---|---|---|
| Year | ||
| 1880 | 90994 | 110490 |
| 1881 | 91953 | 100743 |
| 1882 | 107847 | 113686 |
| 1883 | 112319 | 104625 |
| 1884 | 129019 | 114442 |
px.line(year_sex)
year_sex_unique = pd.pivot_table(babynames,
index=['Year'],
columns=['Sex'],
values='Name',
aggfunc=lambda x: len(np.unique(x)),
)
px.line(year_sex_unique)
Some observations:
name_sex = pd.pivot_table(babynames, index='Name', columns='Sex', values='Count',
aggfunc='sum', fill_value=0., margins=True)
name_sex.head()
| Sex | F | M | All |
|---|---|---|---|
| Name | |||
| aaban | 0 | 120 | 120 |
| aabha | 40 | 0 | 40 |
| aabid | 0 | 16 | 16 |
| aabidah | 5 | 0 | 5 |
| aabir | 0 | 10 | 10 |
Compute proportion of female babies given each name.
prop_female = (name_sex['F'] / name_sex['All']).rename("Prop. Female")
prop_female.head(10)
Name aaban 0.0 aabha 1.0 aabid 0.0 aabidah 1.0 aabir 0.0 aabriella 1.0 aada 1.0 aadam 0.0 aadan 0.0 aadarsh 0.0 Name: Prop. Female, dtype: float64
prop_female['joey']
0.1133165658350894
prop_female['andrew']
0.0037693802316265735
prop_female['avery']
0.6982059396810094
prop_female["min"]
0.37598736176935227
prop_female["pat"]
0.600140600694029
We can define a function to return the most likely Sex for a name. If there is an exact tie or the name does not appear in the social security dataset the function returns Unknown.
def sex_from_name(name):
lower_name = name.lower()
if lower_name not in prop_female.index or prop_female[lower_name] == 0.5:
return "Unknown"
elif prop_female[lower_name] > 0.5:
return "F"
else:
return "M"
sex_from_name("nora")
'F'
sex_from_name("joey")
'M'
names['Pred. Sex'] = names['Name'].apply(sex_from_name)
px.bar(names['Pred. Sex'].value_counts()/len(names))
print("Fraction of names in the babynames data:",
names["Name"].isin(prop_female.index).mean())
Fraction of names in the babynames data: 0.8715596330275229
Why might these names not appear?
names[~names["Name"].isin(prop_female.index)]
| Name | Pred. Sex | |
|---|---|---|
| 14 | baturay | Unknown |
| 43 | subham | Unknown |
| 62 | jihee | Unknown |
| 65 | qilu | Unknown |
| 87 | yike | Unknown |
| ... | ... | ... |
| 1053 | haiyue | Unknown |
| 1062 | risheek | Unknown |
| 1066 | huanran | Unknown |
| 1068 | zefu | Unknown |
| 1079 | dayawanti | Unknown |
140 rows × 2 columns
Previously we treated a name which is given to females 40% of the time as a "Male" name. This doesn't capture our uncertainty. We can use simulation to provide a better distributional estimate.
names["Prop. Female"] = (
names[["Name"]].merge(prop_female, how='left', left_on="Name",
right_index=True)["Prop. Female"]
.fillna(0.5)
)
names.head(10)
| Name | Pred. Sex | Prop. Female | |
|---|---|---|---|
| 0 | andrew | M | 0.003769 |
| 1 | justin | M | 0.004855 |
| 2 | michael | M | 0.004952 |
| 3 | justin | M | 0.004855 |
| 4 | michael | M | 0.004952 |
| 5 | russell | M | 0.004762 |
| 6 | donna | F | 0.997320 |
| 7 | jessica | F | 0.996595 |
| 8 | andrew | M | 0.003769 |
| 9 | emily | F | 0.997951 |
names['Sim. Female'] = names['Prop. Female'] > np.random.rand(len(names))
names.tail(20)
| Name | Pred. Sex | Prop. Female | Sim. Female | |
|---|---|---|---|---|
| 1070 | william | M | 0.003851 | False |
| 1071 | queenie | F | 1.000000 | True |
| 1072 | vinay | M | 0.000000 | False |
| 1073 | ariel | F | 0.792324 | True |
| 1074 | advait | M | 0.000000 | False |
| 1075 | kelly | F | 0.852331 | True |
| 1076 | sanath | M | 0.000000 | False |
| 1077 | armando | M | 0.004982 | False |
| 1078 | quoc | M | 0.000000 | False |
| 1079 | dayawanti | Unknown | 0.500000 | False |
| 1080 | yun | F | 0.750000 | True |
| 1081 | nishita | F | 1.000000 | True |
| 1082 | khanh | M | 0.414427 | False |
| 1083 | amaury | M | 0.003849 | False |
| 1084 | gloria | F | 0.995803 | True |
| 1085 | marshall | M | 0.012124 | False |
| 1086 | aaron | M | 0.007320 | False |
| 1087 | kareena | F | 1.000000 | True |
| 1088 | shervin | M | 0.000000 | False |
| 1089 | leonel | M | 0.000237 | False |
# function that performs many simulations
def simulate_class(students):
is_female = names['Prop. Female'] > np.random.rand(len(names['Prop. Female']))
return np.mean(is_female)
sim_frac_female = np.array([simulate_class(names) for n in range(10000)])
ff.create_distplot([sim_frac_female], ['Fraction Female'], bin_size=0.0025, show_rug=False)