import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_context("talk")
%matplotlib inline
import plotly.offline as py
py.init_notebook_mode(connected=False)
import plotly.graph_objs as go
import plotly.figure_factory as ff
import cufflinks as cf
cf.set_config_file(offline=False, world_readable=True, theme='ggplot')
Feature Engineering¶
In this notebook we will explore a key part of data science, feature engineering: the process of transforming the representation of model inputs to enable better model approximation. Feature engineering enables you to:
- encode non-numeric features to be used as inputs to common numeric models
- capture domain knowledge (e.g., the perceived loudness or sound is the log of the intensity)
- transform complex relationships into simple linear relationships
Mapping from Domain to Range¶
In the supervised learning setting were are given $(X,Y)$ pairs with the goal of learning the mapping from $X$ to $Y$. For example, given pairs of square footage and price we want to learn a function that captures (or at least approximates) the relationship between square feet and price. Our functional approximation is some form of typically parametric mapping from some domain to some range:
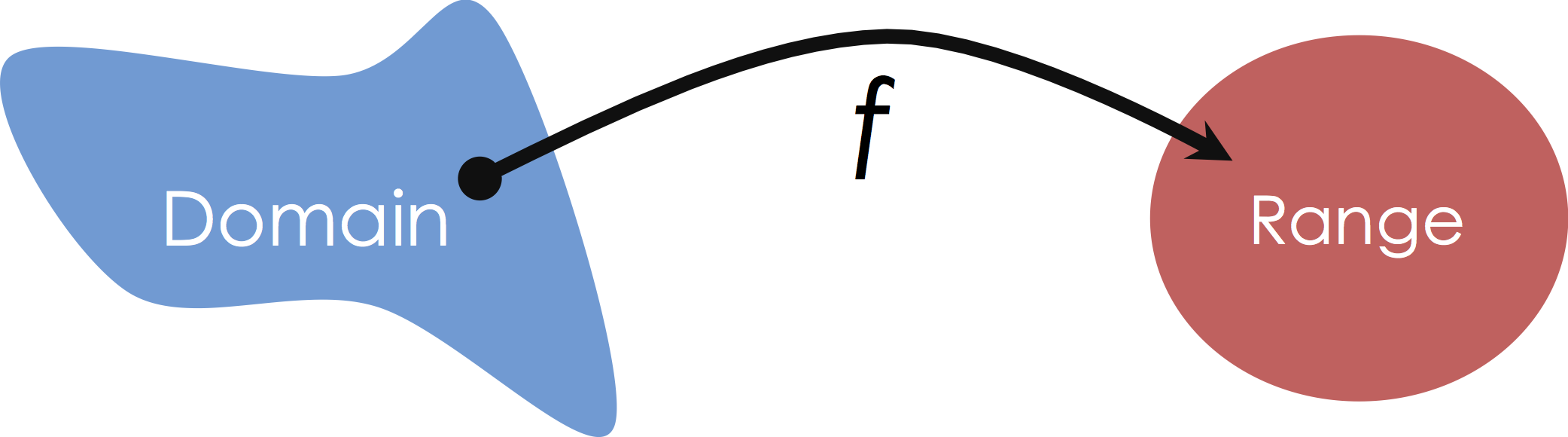
In this class we will focus on Multiple Regression in which we consider mappings from potentially high-dimensional input spaces onto the real line (i.e., $y \in \mathbb{R}$):
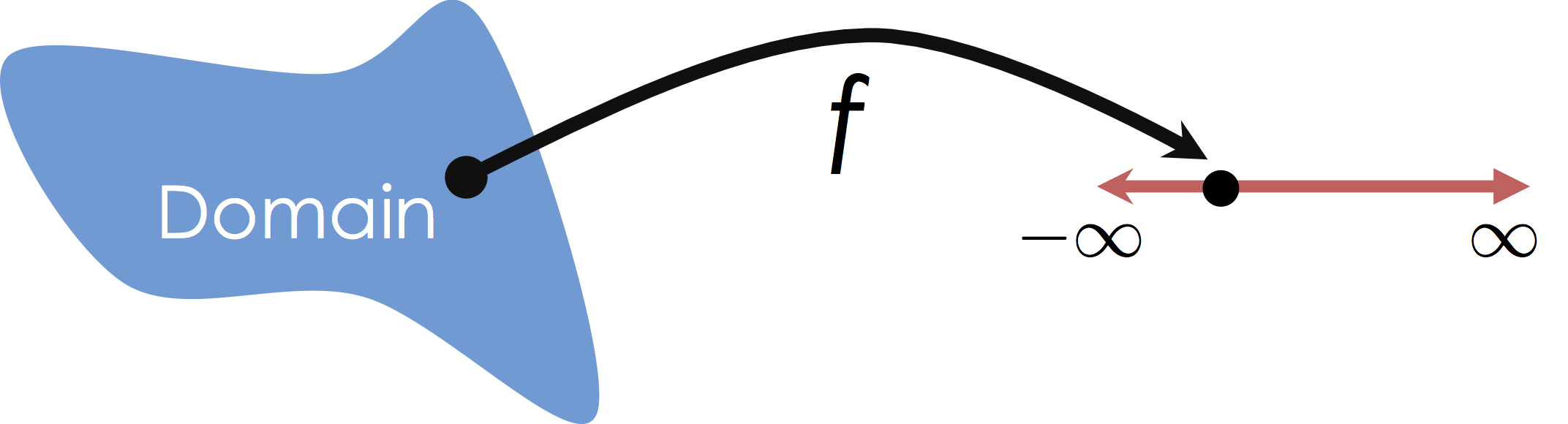
It is worth noting that this is distinct from Multivariate Regression in which we are predicting multiple (confusing?) response values (e.g., $y \in \mathbb{R}^q$).
Not all Domains are Quantitative¶
Suppose we are given the following table:

Our goal is to learn a function that approximates the relationship between the blue and red columns. Let's assume the range, "Ratings", are the real numbers (this may be a problem if ratings are between [0, 5] but more on that later).
What is the domain of this function?
The schema of the relational model provides one possible answer:
RatingsData(uid INTEGER, age FLOAT,
state VARCHAR, hasBought BOOLEAN,
review VARCHAR, rating FLOAT)
Which would suggest that the domain is then:
integers, real numbers, strings, booleans, and more strings.
Unfortunately, the techniques we have discussed so far and most of the techniques in machine learning and statistics operate on real-valued vector inputs $x \in \mathbb{R}^d$ (or for the statisticians $x \in \mathbb{R}^p$).
Goal:¶
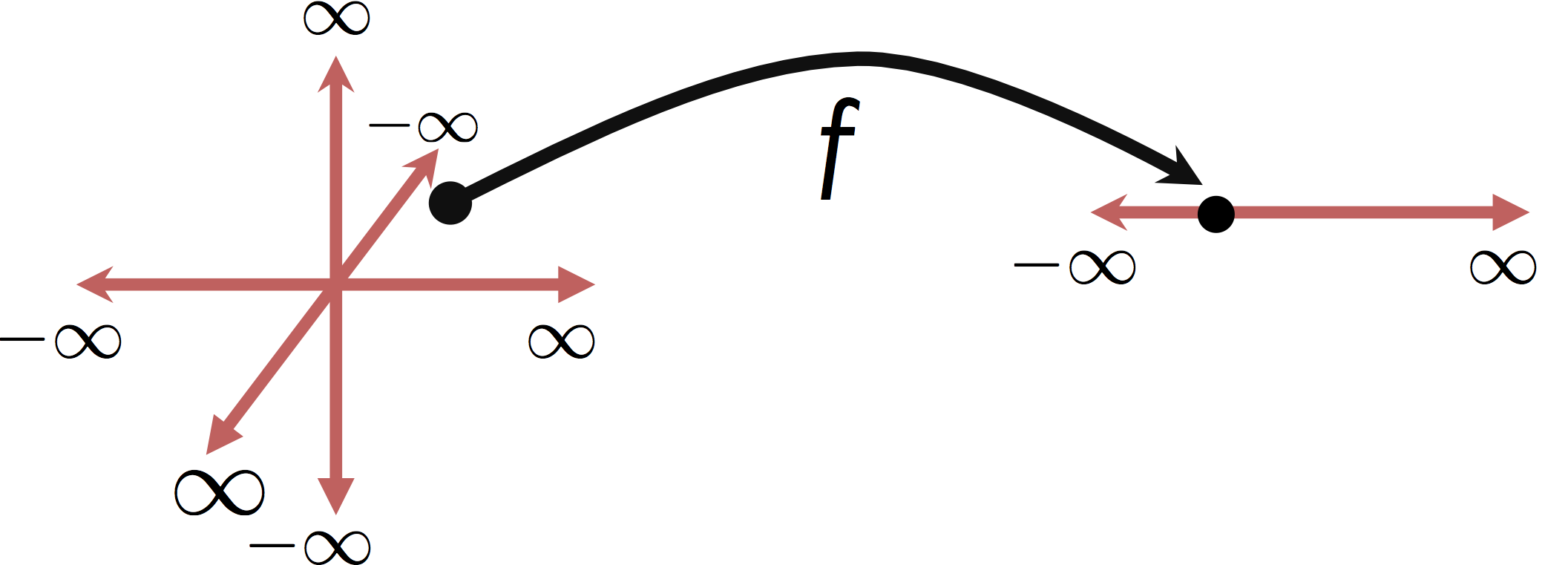
Moreover, many of these techniques, especially the linear models we have been studying, assume the inputs are qauntitative variables in which the relative magnitude of the feature encode information about the response variable.
In the following we define several basic transformations to encode features as real numbers.
Basic Feature Engineering: Get $\mathbb{R}$¶
Our first step as feature engineers is to translate our data into a form that encodes each feature as a continuous variable.
The Uninformative Feature: uid¶
The uid was likely used to join the user information (e.g., age, and state) with some Reviews table. The uid presents several questions:
- What is the meaning of the
uidnumber? - Does the magnitude of the
uidreveal information about the rating?
There are several answers:
Although numbers, identifiers are typically categorical (like strings) and as a consequence the magnitude has little meaning. In these settings we would either drop or one-hot encode the
uid. We will return to feature dropping and one-hot-encoding in a moment.There are scenarios where the magnitude of the numerical
uidvalue contains important information. When user ids are created in consecutive order, larger user ids would imply more recent users. In these cases we might to interpret theuidfeature as a real number and keep it in our model.
Dropping Features¶
While uncommon there are certain scenarios where manually dropping features might be helpful:
when the features does not to contain information associated with the prediction task. Dropping uninformative features can help to address over-fitting, an issue we will discuss in great detail soon.
when the feature is not available at prediction time. For example, the feature might contain information collected after the user entered a rating. This is a common scenario in time-series analysis.
However, in the absence of substantial domain knowledge, we would prefer to use algorithmic techniques to help eliminate features. We will discuss this in more detail when we return to regularization.
The Continuous age Feature¶
The age feature encodes the users age. This is already a continuous real number so no additional feature transformations are required. However, as we will soon see, we may introduce additional related features (e.g., indicators for various age groups or non-linear transformations).
The Categorical state Feature¶
The state feature is a string encoding the category (one of the 50 states). How do we meaningfully encode such a feature as one or more real-numbers?
We could enumerate the states in alphabetical order AL=0, AK=2, ... WY=49. This is a form of dictionary encoding which maps each category to an integer. However, this would likely be a poor feature encoding since the magnitude provides little information about the rating.
Alternatively, we might enumerate the states based on their geographic region (e.g., lower numbers for coastal states.). While this alternative dictionary encoding may provide information there is better way to encode categorical features for machine learning algorithms.
One-Hot Encoding¶
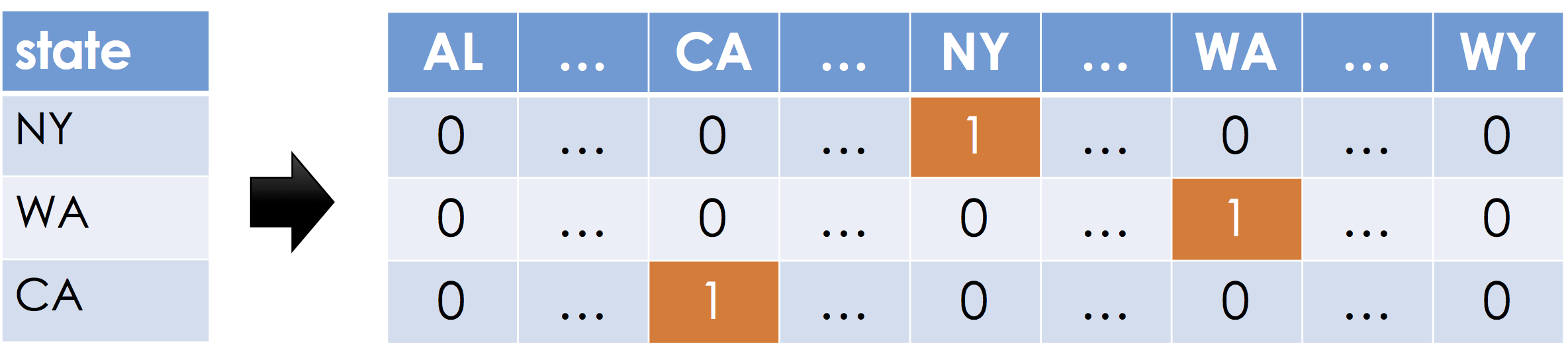
One-Hot encoding, sometimes also called dummy encoding is a simple mechanism to encode categorical data as real numbers such that the magnitude of each dimension is meaningful. Suppose a feature can take on $k$ distinct values (e.g., $k=50$ for 50 states in the United Stated). For each distinct possible value a new feature (dimension) is created. For each record, all the new features are set to zero except the one corresponding to the value in the original feature.
The term one-hot encoding comes from a digital circuit encoding of a categorical state as particular "hot" wire:
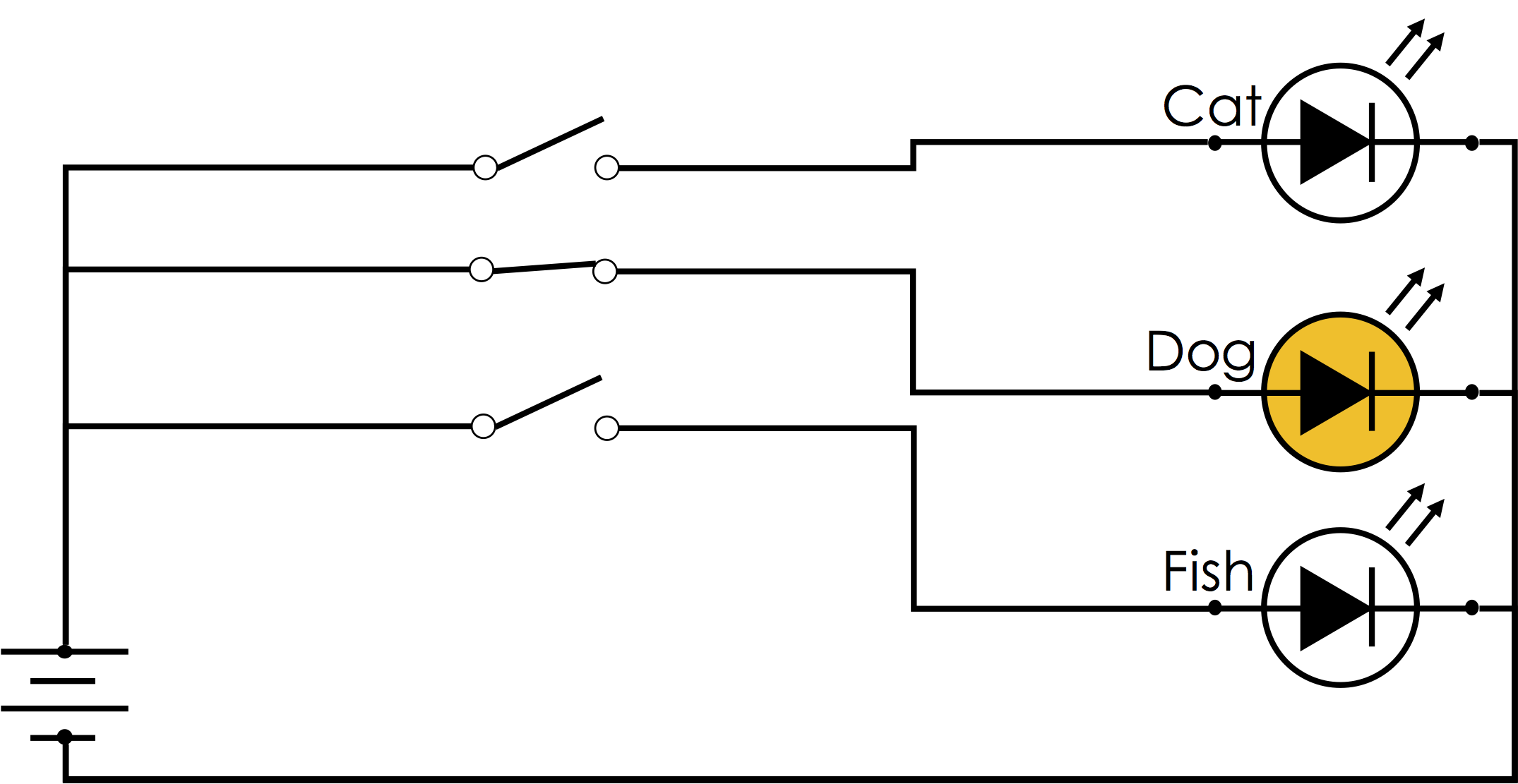
One-Hot Encoding in Pandas¶
Here we create a toy DataFrame of pets including their name and kind:
df = pd.DataFrame({
"name": ["Goldy", "Scooby", "Brian", "Francine", "Goldy"],
"kind": ["Fish", "Dog", "Dog", "Cat", "Dog"],
"age": [0.5, 7., 3., 10., 1.]
}, columns = ["name", "kind", "age"])
df
Pandas has a built in function to construct one-hot encodings called get_dummies
pd.get_dummies(df['kind'])
pd.get_dummies(df)
A serious issue with using Pandas to construct a one-hot-encoding is that if we get new dat in a different DataFrame we may get a different encoding. Scikit-learn provides more flexible routines to construct features.
One-Hot Encoding in Scikit-Learn¶
Scikit-Learn also has several library for constructing one-hot-encodings.
from sklearn.feature_extraction import DictVectorizer
vec_enc = DictVectorizer()
vec_enc.fit(df.to_dict(orient='records'))
vec_enc.transform(df.to_dict(orient='records')).toarray()
vec_enc.get_feature_names()
Applying to new data¶
One advantage of the DictVectorizer in sklearn is that we can easily apply it to new data:
vec_enc.transform([
{"kind": "Cat", "name": "Goldy", "age": 35},
{"kind": "Bird", "name": "Fluffy"},
{"breed": "Chihuahua", "name": "Goldy"},
]).toarray()
The Text review Feature¶
Encoding text as a real-valued feature is especially challenging and many of the standard transformations are lossy. Moreover, all of the earlier transformations (e.g., one-hot encoding and Boolean representations) preserve the information in the feature. In contrast, most of the techniques for encoding text destroy information about the word order and in many cases key parts of the grammar.
Here we will discuss two widely used representations of text:
- Bag-of-Words Encoding: encodes text by the frequency of each word
- N-Gram Encoding: encodes text by the frequency of sequences of words of length $N$
Both of these encoding strategies are related to the one-hot encoding with dummy features created for every word or sequence of words and with multiple dummy features having counts greater than zero.
The Bag-of-Words Encoding¶
The bag-of-words encoding is widely used and a standard representation for text in many of the popular text clustering algorithms. The following is a simple illustration of the bag-of-words encoding:
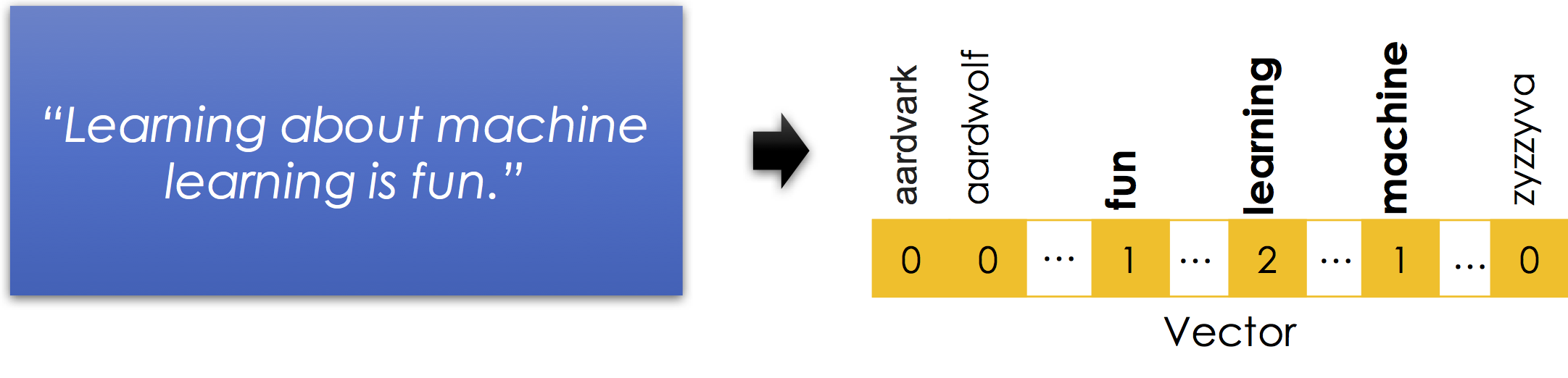
Notice
- Stop words are removed. Stop-words are words like
isandaboutthat in isolation contain very little information about the meaning of the sentence. Here is a good list of stop-words in many languages. - Word order information is lost. Nonetheless the vector still suggests that the sentence is about
fun,machines, andlearning. Thought there are many possible meanings learning machines have fun learning or learning about machines is fun learning ... - Capitalization and punctuation are typically removed.
- Sparse Encoding: is necessary to represent the bag-of-words efficiently. There are millions of possible words (including terminology, names, and misspellings) and so instantiating a
0for every word that is not in each record would be incredibly inefficient.
Why is it called a bag-of-words? A bag is another term for a multiset: an unordered collection which may contain multiple instances of each element.
Professor Gonzalez is an "artist"¶
When professor Gonzalez was a graduate student at Carnegie Mellon University, he and several other computer scientists created the following art piece on display in the Gates Center:

Is this art or science?
Notice
- The unordered collection of words in the bag.
- The stop words on the floor.
- The missing broom. The original sculpture had a broom attached but the janitor got confused ....
Implementing the Bag-of-words Model¶
We can use sklearn to construct a bag-of-words representation of text
frost_text = [x for x in """
Some say the world will end in fire,
Some say in ice.
From what Ive tasted of desire
I hold with those who favor fire.
""".split("\n") if len(x) > 0]
frost_text
from sklearn.feature_extraction.text import CountVectorizer
# Construct the tokenizer with English stop words
bow = CountVectorizer(stop_words="english")
# fit the model to the passage
bow.fit(frost_text)
# Print the words that are kept
print("Words:", list(enumerate(bow.get_feature_names())))
print("Sentence Encoding: \n")
# Print the encoding of each line
for (s, r) in zip(frost_text, bow.transform(frost_text)):
print(s)
print(r)
print("------------------")
The N-Gram Encoding¶
The N-Gram encoding is a generalization of the bag-of-words encoding designed to capture limited ordering information. Consider the following passage of text:
The book was not well written but I did enjoy it.
If we re-arrange the words we can also write:
The book was well written but I did not enjoy it.
Moreover, local word order can be important when making decisions about text. The n-gram encoding captures local word order by defining counts over sliding windows. In the following example a bi-gram ($n=2$) encoding is constructed:
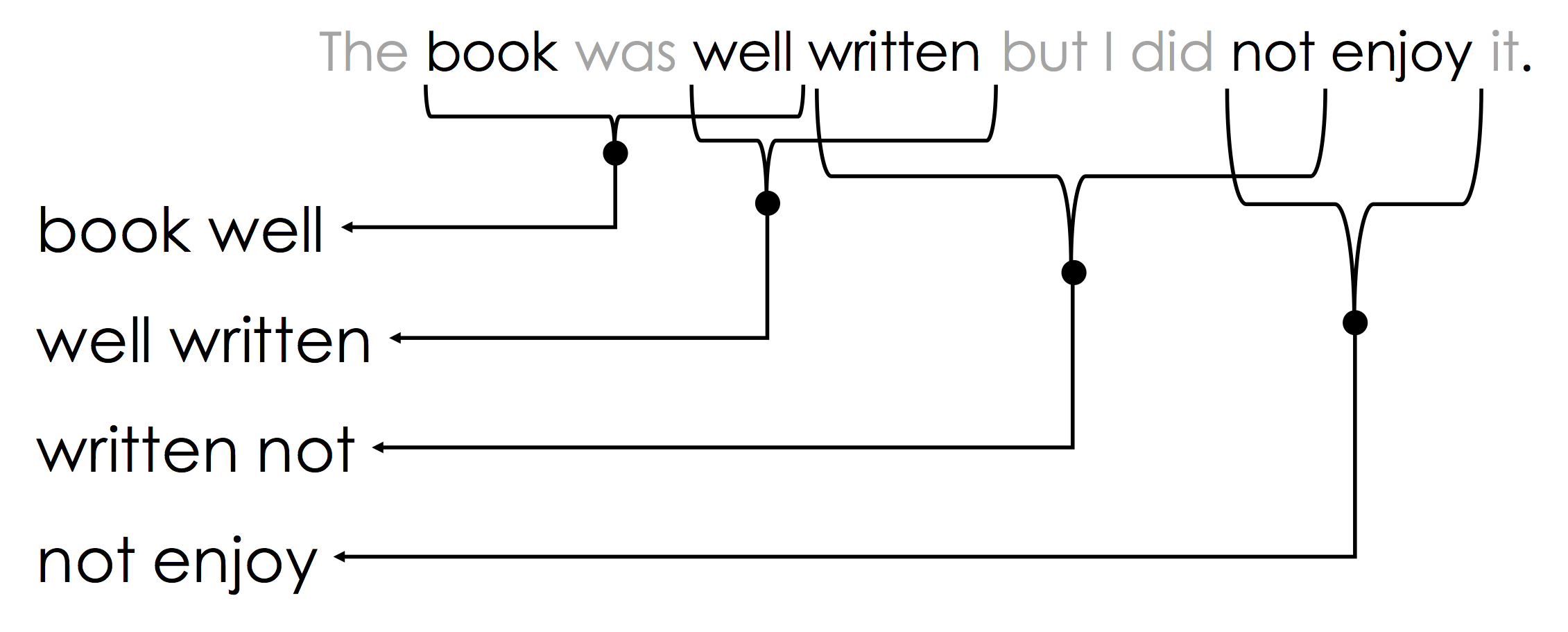
The above n-gram would be encoded in the sparse vector:
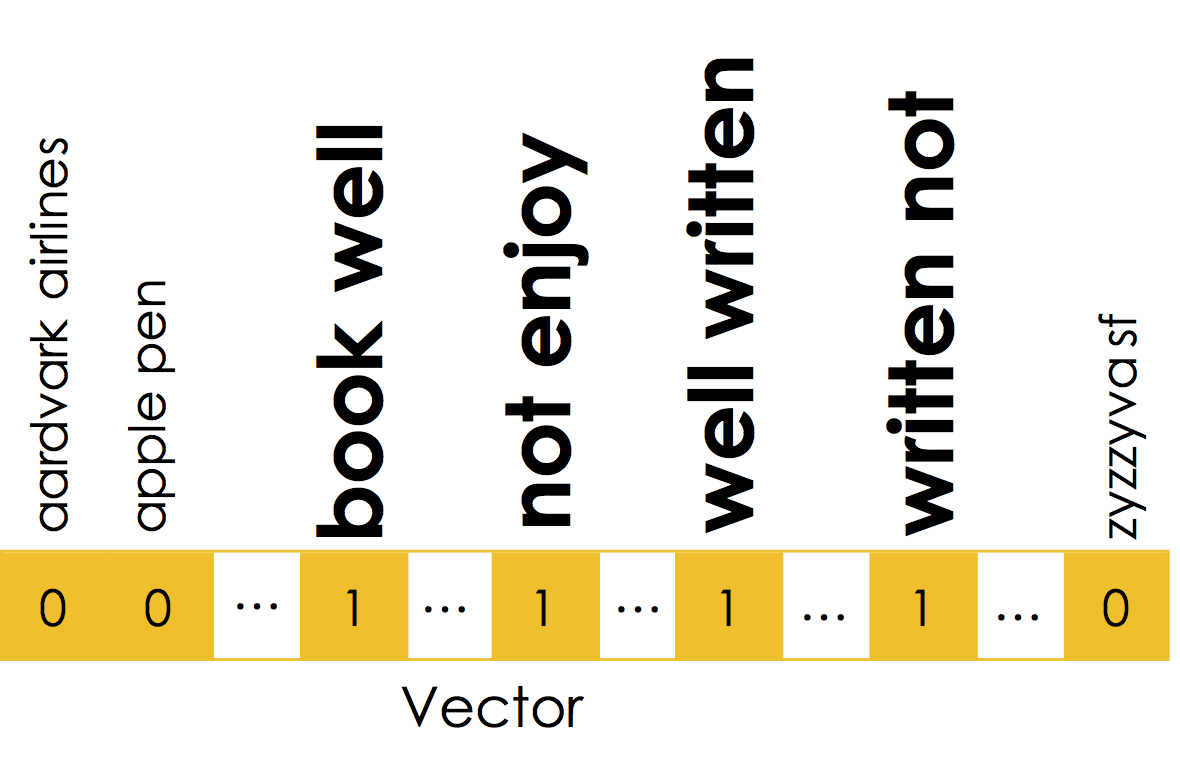
Notice that the n-gram captures key pieces of sentiment information: "well written" and "not enjoy".
N-grams are often used for other types of sequence data beyond text. For example, n-grams can be used to encode genomic data, protein sequences, and click logs.
N-Gram Issues
- The n-gram representation is hyper sparse and maintaining the dictionary of possible n-grams can be very costly. The hashing trick is a popular solution to approximate the sparse n-gram encoding. In the hashing trick each n-gram is mapped to a relatively large (e.g., 32bit) hash-id and the counts are associated with the hash index without saving the n-gram text in a dictionary. As a consequence, multiple n-grams are treated as the same.
- As $N$ increase the chance of seeing the same n-grams at prediction time decreases rapidly.
# Construct the tokenizer with English stop words
bigram = CountVectorizer(ngram_range=(1, 2))
# fit the model to the passage
bigram.fit(frost_text)
# Print the words that are kept
print("\nWords:",
list(zip(range(0,len(bigram.get_feature_names())), bigram.get_feature_names())))
print("\nSentence Encoding: \n")
# Print the encoding of each line
for (s, r) in zip(frost_text, bigram.transform(frost_text)):
print(s)
print(r)
print("------------------")
Non-linear Relationships¶
For this exercise we are going to use synthetic data to illustrate the basic ideas of model design. Notice here that we are generating data from a linear model with Gaussian noise.
train_data = pd.read_csv("data/toy_training_data.csv")
train_data.head()
# Visualize the data ---------------------
train_points = go.Scatter(name = "Training Data",
x = train_data['X'], y = train_data['Y'],
mode = 'markers')
# layout = go.Layout(autosize=False, width=800, height=600)
py.iplot(go.Figure(data=[train_points]))
Is this data linear?¶
How would you describe this data?
- Is there a linear relationship between $X$ and $Y$?
- Are there other patterns?
- How noisy is the data?
- Do we see obvious outliers?
The relationship between X and Y does appear to have some linear trend but there also appears to be other patterns in the relationship?
However, in this lecture we will show that linear models can still be used to model this data very effectively.
Yes! Let's see how.
What does it mean to be a linear model¶
Let's return to what it means to be a linear model:
$$\large f_\theta(x) = x^T \theta = \sum_{j=1}^p x_j \theta_j $$
In what sense is the above model linear?
- Linear in the features $x$?
- Linear in the parameters $\theta$?
- Linear in both at the same time?
Yes, Yes, and No. If we look at just the features or just the parameters the model is linear. However, if we look at both at the same time it is not. Why?
Feature Functions¶
Consider the following alternative model formulation:
$$\large f_\theta\left( x \right) = \phi(x)^T \theta = \sum_{j=1}^{k} \phi_j(x) \theta_j $$
where $\phi_j$ is an arbitrary function from $x\in \mathbb{R}^p$ to $\phi(x)_j \in \mathbb{R}$ and we define $k$ of these functions. We often refer to these functions $\phi_j$ as feature functions or basis functions and their design plays a critical role in both how we capture prior knowledge and our ability to fit complicated data.
The Transformed Covariate Matrix¶
As a consequence, while the model $f_\theta\left(x \right)$ is no longer linear in $x$ it is still a linear model because it is linear in $\theta$. This means we can continue to use the normal equations to compute the optimal parameters.
Minimizing the squared loss (not shown) we obtain the normal equation:
$$ \large \hat{\theta} = \left( \Phi^T \Phi \right)^{-1} \Phi^T Y $$
It is worth noting that the model is also linear in $\phi$ and that the $\phi_j$ form a new basis (hence the term basis functions) in which the data live. As a consequence we can think of $\phi$ as mapping the data into a new (often higher dimensional space) in which the relationship between $y$ and $\phi(x)$ is defined by a hyperplane.
Capturing Domain Knowledge¶
Feature functions can be used to capture domain knowledge by:
- Introducing additional information from other sources
- Combining related features
- Encoding non-linear patterns
Suppose I had data about customer purchases and I wanted to estimate their income:
\begin{align} \phi(\text{date}, \text{lat}, \text{lon}, \text{amount})_1 &= \textbf{isWinter}(\text{date}) \\ \phi(\text{date}, \text{lat}, \text{lon}, \text{amount})_2 &= \cos\left( \frac{\textbf{Hour}(\text{date})}{12} \pi \right) \\ \phi(\text{date}, \text{lat}, \text{lon}, \text{amount})_3 &= \frac{\text{amount}}{\textbf{avg_spend}[\textbf{ZipCode}[\text{lat}, \text{lon}]]} \\ \phi(\text{date}, \text{lat}, \text{lon}, \text{amount})_4 &= \exp\left(-\textbf{Distance}\left((\text{lat},\text{lon}), \textbf{StoreA}\right)\right)^2 \\ \phi(\text{date}, \text{lat}, \text{lon}, \text{amount})_5 &= \exp\left(-\textbf{Distance}\left((\text{lat},\text{lon}), \textbf{StoreB}\right)\right)^2 \end{align}
Notice: In the above feature functions:
- The transformations are non-linear
- They pull in additional information
- They may encode implicit knowledge
- The functions $\phi$ do not depend on $\theta$
Transforming the Toy Data¶
In our toy data set we observed a cyclic pattern. Here we construct a $\phi$ to capture the cyclic nature of our data and visualize the corresponding hyperplane.
In the following cell we define a function $\phi$ that maps $x\in \mathbb{R}$ to the vector $[x,\sin(x)] \in \mathbb{R}^2$
$$ \large \phi(x) = [x, \sin(x)] $$
Why not:
$$ \large \phi(x) = [x, \sin(\theta_3 x + \theta_4)] $$
This would no longer be linear $\theta$. However, in practice we might want to consider a range of $\sin$ basis:
$$ \large \phi_{\alpha,\beta}(x) = \sin(\alpha x + \beta) $$
for different values of $\alpha$ and $\beta$. The parameters $\alpha$ and $\beta$ are typically called hyperparameters because (at least in this setting) they are not set automatically through learning.
def sin_phi(x):
return np.hstack([x, np.sin(x)])
Phi = sin_phi(train_data[["X"]])
Phi[:5]
Fit a Linear Model on $\Phi$¶
We can again use the scikit-learn package to fit a linear model on the transformed space.
Fitting the Basic Linear Model¶
from sklearn import linear_model
basic_reg = linear_model.LinearRegression(fit_intercept=True)
basic_reg.fit(train_data[['X']], train_data['Y'])
Fitting the Transformed Linear Model on $\Phi$¶
from sklearn import linear_model
sin_reg = linear_model.LinearRegression(fit_intercept=True)
sin_reg.fit(sin_phi(train_data[["X"]]), train_data['Y'])
Making Predictions at Query Locations¶
X_query = np.linspace(train_data['X'].min()-1, train_data['X'].max() +1, 100)
Y_basic_query = basic_reg.predict(X_query[:, np.newaxis])
Y_sin_query = sin_reg.predict(sin_phi(X_query[:, np.newaxis]))
Visualizing the Fit¶
# Define the least squares regression line
basic_line = go.Scatter(name = r"Basic Model", x=X_query, y = Y_basic_query)
sin_line = go.Scatter(name = r"Transformed Model", x=X_query, y = Y_sin_query)
# Definethe residual lines segments, a separate line for each
# training point
residual_lines = [
go.Scatter(x=[x,x], y=[y,yhat],
mode='lines', showlegend=False,
line=dict(color='black', width = 0.5))
for (x, y, yhat) in zip(train_data['X'], train_data['Y'],
sin_reg.predict(sin_phi(train_data[["X"]])))
]
# Combine the plot elements
py.iplot([train_points, basic_line, sin_line] + residual_lines)
Linear Model in a Transformed Space¶
As discussed earlier the model we just constructed, while non-linear in $x$ is actually a linear model in $\phi(x)$ and we can visualize that linear model's structure in higher dimensions.
# Plot the data in higher dimensions
phi3d = go.Scatter3d(name = "Raw Data",
x = Phi[:,0], y = Phi[:,1], z = train_data['Y'],
mode = 'markers',
marker = dict(size=3),
showlegend=False
)
# Compute the predictin plane
(u,v) = np.meshgrid(np.linspace(-10,10,5), np.linspace(-1,1,5))
coords = np.vstack((u.flatten(),v.flatten())).T
ycoords = sin_reg.predict(coords)
fit_plane = go.Surface(name = "Fitting Hyperplane",
x = np.reshape(coords[:,0], (5,5)),
y = np.reshape(coords[:,1], (5,5)),
z = np.reshape(ycoords, (5,5)),
opacity = 0.8, cauto = False, showscale = False,
colorscale = [[0, 'rgb(255,0,0)'], [1, 'rgb(255,0,0)']]
)
# Construct residual lines
Yhat = sin_reg.predict(Phi)
residual_lines = [
go.Scatter3d(x=[x[0],x[0]], y=[x[1],x[1]], z=[y, yhat],
mode='lines', showlegend=False,
line=dict(color='black'))
for (x, y, yhat) in zip(Phi, train_data['Y'], Yhat)
]
# Label the axis and orient the camera
layout = go.Layout(
scene=go.Scene(
xaxis=go.XAxis(title='X'),
yaxis=go.YAxis(title='sin(X)'),
zaxis=go.ZAxis(title='Y'),
aspectratio=dict(x=1.,y=1., z=1.),
camera=dict(eye=dict(x=-1, y=-1, z=0))
)
)
py.iplot(go.Figure(data=[phi3d, fit_plane] + residual_lines, layout=layout))
Error Estimates¶
How well are we fitting the data? We can compute the root mean squared error.
def rmse(y, yhat):
return np.sqrt(np.mean((yhat-y)**2))
basic_rmse = rmse(train_data['Y'], basic_reg.predict(train_data[['X']]))
sin_rmse = rmse(train_data['Y'], sin_reg.predict(sin_phi(train_data[['X']])))
py.iplot(go.Figure(data =[go.Bar(
x=[r'Basic Regression',
r'Sine Transformation'],
y=[basic_rmse, sin_rmse]
)], layout = go.Layout(title="Loss Comparison",
yaxis=dict(title="RMSE"))))
Generic Feature Functions¶
We will now explore a range of generic feature transformations. However, before we proceed it is worth contrasting two categories of feature functions and their applications.
Interpretable Features: In settings where our goal is to understand the model (e.g., identify important features that predict customer churn) we may want to construct meaningful features based on our understanding of the domain.
Generic Features: However, in other settings where our primary goals is to make accurate predictions we may instead introduce generic feature functions that enable our models to fit and generalize complex relationships.
Gaussian Radial Basis Functions¶
One of the more widely used generic feature functions are Gaussian radial basis functions. These feature functions take the form:
$$ \phi_{(\lambda, u_1, \ldots, u_k)}(x) = \left[\exp\left( - \frac{\left|\left|x-u_1\right|\right|_2^2}{\lambda} \right), \ldots, \exp\left( - \frac{\left|\left| x-u_k \right|\right|_2^2}{\lambda} \right) \right] $$
The hyper-parameters $u_1$ through $u_k$ and $\lambda$ are not optimized with $\theta$ but instead are set externally. In many cases the $u_i$ may correspond to points in the training data. The term $\lambda$ defines the spread of the basis function and determines the "smoothness" of the function $f_\theta(\phi(x))$.
The following is a plot of three radial basis function centered at 2 with different values of $\lambda$.
def gaussian_rbf(u, lam=1):
return lambda x: np.exp(-(x - u)**2 / lam**2)
tmpX = np.linspace(-2, 6,1000)
py.iplot([
dict(name=r"$\lambda=0.5$", x=tmpX,
y=gaussian_rbf(2, lam=0.5)(tmpX)),
dict(name=r"$\lambda=1$", x=tmpX,
y=gaussian_rbf(2, lam=1.)(tmpX)),
dict(name=r"$\lambda=2$", x=tmpX,
y=gaussian_rbf(2, lam=2.)(tmpX))
])
Develop some helper code¶
To simplify the following analysis we create two helper functions.
uniform_rbf_phiwhich constructs uniformly spaced RBF functions and each function is a feature that has a large value when the input $x$ is nearby.evaluate_basiswhich takes a feature function configuration and fits a model
def uniform_rbf_phi(x, lam=1, num_basis = 10, minvalue=-9, maxvalue=9):
return np.hstack([gaussian_rbf(u, lam)(x) for u in np.linspace(minvalue, maxvalue, num_basis)])
tmpXTall = np.linspace(-11, 11,1000)[:,np.newaxis]
py.iplot([
dict(name=r"$\lambda=0.1$", x=tmpXTall[:,0],
y=uniform_rbf_phi(tmpXTall, lam=0.1).mean(axis=1)),
dict(name=r"$\lambda=0.5$", x=tmpXTall[:,0],
y=uniform_rbf_phi(tmpXTall, lam=0.5).mean(axis=1)),
dict(name=r"$\lambda=1$", x=tmpXTall[:,0],
y=uniform_rbf_phi(tmpXTall, lam=1.).mean(axis=1)),
])
def evaluate_basis(phi, desc):
# Apply transformation
Phi = phi(train_data[["X"]])
# Fit a model
reg_model = linear_model.LinearRegression(fit_intercept=True)
reg_model.fit(Phi, train_data['Y'])
# Create plot line
X_test = np.linspace(-11, 11, 1000) # Fine grained test X
Phi_test = phi(X_test[:,np.newaxis])
Yhat_test = reg_model.predict(Phi_test)
line = go.Scatter(name = desc, x=X_test, y=Yhat_test)
# Compute RMSE
Yhat = reg_model.predict(Phi)
error = rmse(train_data['Y'], Yhat)
# return results
return (line, error, reg_model)
Visualizing 10 RBF features¶
(rbf_line10, rbf_rmse10, rbf_reg10) = \
evaluate_basis(lambda x: uniform_rbf_phi(x, lam=1, num_basis=10), r"RBF10")
py.iplot([train_points, rbf_line10, basic_line, sin_line])
Visualizing 50 RBF features (Really Connecting the Dots!)¶
We are now getting a really good fit to this dataset!!!!
(rbf_line50, rbf_rmse50, rbf_reg50) = \
evaluate_basis(lambda x: uniform_rbf_phi(x, lam=0.3, num_basis=50), r"RBF50")
fig = go.Figure(data=[train_points, rbf_line50, rbf_line10, sin_line, basic_line ],
layout = go.Layout(xaxis=dict(range=[-10,10]),
yaxis=dict(range=[-10,50])))
py.iplot(fig)
Examining the Error¶
train_bars = go.Bar(
x=[r'Basic Regression',
r'Sine Transformation',
r'RBF 10',
r'RBF 50'],
y=[basic_rmse, sin_rmse, rbf_rmse10, rbf_rmse50],
name="Training Erorr")
py.iplot(go.Figure(data = [train_bars], layout = go.Layout(title="Loss Comparison",
yaxis=dict(title="RMSE"))))
Which is the best model?¶
We started with the objective of minimizing the training loss (error). As we increased the model sophistication by adding features we were able to fit increasingly complex functions to the data and reduce the loss. However, is our ultimate goal to minimize training error?
Ideally we would like to minimize the error we make when making new predictions at unseen values of $X$. One way to evaluate that error is use a test dataset which is distinct from the dataset used to train the model. Fortunately, we have such a test dataset.
test_data = pd.read_csv("data/toy_test_data.csv")
test_points = go.Scatter(name = "Test Data", x = test_data['X'], y = test_data['Y'],
mode = 'markers', marker=dict(symbol="cross", color="red"))
py.iplot([train_points, test_points])
def test_rmse(phi, reg):
return rmse(test_data['Y'], reg.predict(phi(test_data[['X']])))
test_bars = go.Bar(
x=[r'Basic Regression',
r'Sin Transformation',
r'RBF 10',
r'RBF 50'],
y=[test_rmse(lambda x: x, basic_reg),
test_rmse(sin_phi, sin_reg),
test_rmse(lambda x: uniform_rbf_phi(x, lam=1, num_basis=10), rbf_reg10),
test_rmse(lambda x: uniform_rbf_phi(x, lam=0.3, num_basis=50), rbf_reg50)
],
name="Test Error"
)
py.iplot(go.Figure(data =[train_bars, test_bars], layout = go.Layout(title="Loss Comparison",
yaxis=dict(title="RMSE"))))
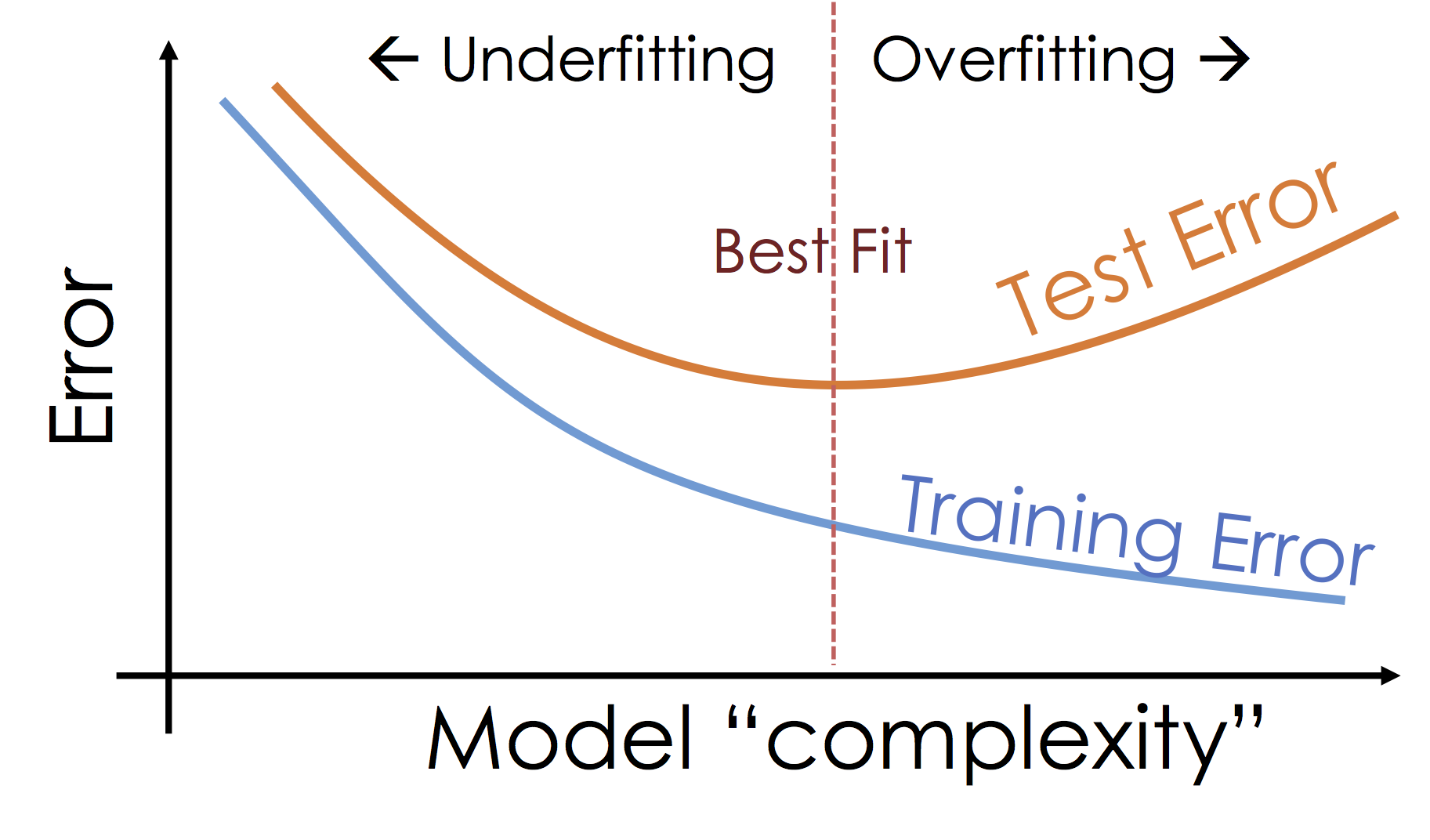
What's happening: Over-fitting¶
As we increase the expressiveness of our model we begin to over-fit to the variability in our training data. That is we are learning patterns that do not generalize beyond our training dataset
Over-fitting is a key challenge in machine learning and statistical inference. At it's core is a fundamental trade-off between bias and variance: the desire to explain the training data and yet be robust to variation in the training data.
We will study the bias-variance trade-off more in the next lecture but for now we will focus on the trade-off between under fitting and over fitting:
Train, Test, and Validation Split¶
To manage over-fitting it is essential to split your initial training data into a training and testing dataset.

The Train - Test Split¶
Before running cross validation split the data into train and test subsets (typically a 90-10 split). How should you do this? You want the test data to reflect the prediction goal:
- Random sample of the training data
- Future examples
- Different stratifications
Ask yourself, where will I be using this model and how does that relate to my test data.
Do not look at the test data until after selecting your final model. Also, it is very important to not look at the test data until after selecting your final model. Finally, you should not look at the test data until after selecting your final model.
Cross Validation¶
With the remaining training data:
- Split the remaining training dataset k-ways as in the Figure above. The figure uses 5-Fold which is standard. You should split the data in the same way you constructed the test set (this is typically randomly)
- For each split train the model on the training fraction and then compute the error (RMSE) on the validation fraction.
- Average the error across each validation fraction to estimate the test error.
Questions:
- What is this accomplishing?
- What are the implication on the choice of $k$?
Answers:
- This is repeatedly simulating the train-test split we did earlier. We repeat this process because it is noisy.
- Larger $k$ means we average our validation error over more instances which makes our estimate of the test error more stable. This typically also means that the validation set is smaller so we have more training data. However, larger $k$ also means we have to train the model more often which gets computational expensive