Introduction to Bias-Variance tradeoff and regularization¶
A simplified version of the more complete notebook on this topic that we'll use later, once we've had a chance to discuss linear regression and feature engineering.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_context("talk")
%matplotlib inline
import plotly.offline as py
py.init_notebook_mode(connected=False)
from IPython.core.display import display, HTML
# The polling here is to ensure that plotly.js has already been loaded before
# setting display alignment in order to avoid a race condition.
display(HTML(
'<script>'
'var waitForPlotly = setInterval( function() {'
'if( typeof(window.Plotly) !== "undefined" ){'
'MathJax.Hub.Config({ SVG: { font: "STIX-Web" }, displayAlign: "center" });'
'MathJax.Hub.Queue(["setRenderer", MathJax.Hub, "SVG"]);'
'clearInterval(waitForPlotly);'
'}}, 5000 );'
'</script>'
))
import plotly.graph_objs as go
import plotly.figure_factory as ff
import cufflinks as cf
cf.set_config_file(offline=False, world_readable=True, theme='ggplot')
This notebook which accompanies the lecture on the Bias Variance Tradeoff and Regularization.
Notebook created by Joseph E. Gonzalez for DS100.
Toy Dataset¶
As with the previous lectures we will continue to use an easy to visualize synthetic dataset.
rnd_seed = 42
np.random.seed(rnd_seed)
n = 50
sigma = 10
noise = np.random.normal(scale=sigma, size=n)
X = np.random.uniform(-10, 10, n)
Y0 = 100 + 20. * X
Y2 = 100 + 20. * X - 2 * X**2 + noise
Y5 = 100 + 20. * X - 2 * X**2 - 0.6 * X**3 + 0.004 * X**5 + noise
# Choose one of Y0, Y2 or Y5
Y = Y5
data_points = go.Scatter(name="data", x=X, y=Y, mode='markers')
py.iplot([data_points])
Making a Train-Test Split¶
It is always a good habit to split data into training and test sets.
## Train Test Split
from sklearn.model_selection import train_test_split
X_tr, X_te, Y_tr, Y_te = train_test_split(X, Y, test_size=0.5, random_state=rnd_seed)
old_points = go.Scatter(name="Old Data", x=X_tr, y=Y_tr, mode='markers',
marker=dict(color="blue", symbol="o"))
new_points = go.Scatter(name="New Data", x=X_te, y=Y_te, mode='markers',
marker=dict(color="red", symbol="x"))
py.iplot([old_points, new_points])
Polynomial Features:¶
In the following we work through a basic bias variance tradeoff for different numbers of polynomial features. To make things a bit more interesting we will also add an additional sine feature:
$$ \large \Phi_d(x) = \left[x, x^2, \ldots, x^d \right] $$
We use the following Python function to generate a $\Phi$:
def poly_phi(k):
return lambda X: np.array([X ** i for i in range(1, k+1)]).T
Trying different numbers of features¶
We will consider the following basis sizes:
basis_sizes = [1, 2, 5, 8, 16, 24, 32]
Create a $\Phi$ feature matrix for each number of basis:
Phis_tr = { k: poly_phi(k)(X_tr) for k in basis_sizes }
Train a model for each number of feature
from sklearn import linear_model
models = {}
for k in Phis_tr:
model = linear_model.LinearRegression()
model.fit(Phis_tr[k], Y_tr)
models[k] = model
Visualize the various models¶
The following code is a bit complicated but essentially makes an interactive visualization of the various models.
# Make the x values where plot points will be generated
X_plt = np.linspace(np.min(X)-1, np.max(X)+1, 200)
# Generate the Plotly line objects by predicting the value at each X_plt
lines = []
for k in sorted(models.keys()):
ytmp = models[k].predict(poly_phi(k)(X_plt))
# Plotting software fails with large numbers
ytmp[ytmp > 500] = 500
ytmp[ytmp < -500] = -500
lines.append(
go.Scatter(name="degree "+ str(k), x=X_plt,
y = ytmp,visible=False))
# Construct steps for the interactive slider
steps = []
data = [old_points, new_points]
data_visibility = [True, True]
lines[0].visible=True
for i, line in enumerate(lines):
line_visibility = [False] * len(lines)
line_visibility[i] = True # Toggle i'th trace to "visible"
step = dict(
label = line['name'],
method = 'restyle',
args = ['visible', data_visibility + line_visibility],
)
steps.append(step)
# Build the slider object
sliders = [dict(active = 0, pad = {"t": 20}, steps = steps)]
# render the plot
layout = go.Layout(xaxis=dict(range=[np.min(X_plt), np.max(X_plt)]),
yaxis=dict(range=[np.min(Y) -5 , np.max(Y)+5]),
sliders=sliders)
py.iplot(go.Figure(data = data + lines, layout=layout))
Regularization¶
In the previous notebook we adjusted the number of polynomial features to control model complexity and tradeoff bias and variance. However, this approach to managing model complexity has a few critical limitations:
- complexity varies discretely
- we may only need a few of the higher degree polynomial terms
- In general we may not have a natural way to order our basis
Rather than changing the dimension we can instead apply regularization to the weights. More generally, we can adopt the framework of regularized loss minimization.
$$ \large \hat{\theta} = \arg \min_\theta \frac{1}{n} \sum_{i=1}^n \textbf{Loss}\left(y_i, f_\theta(x_i)\right) + \lambda \textbf{R}(\theta) $$
The regularization term $\textbf{R}(\theta)$ penalizes for $\theta$ values that result in more complex and therefore higher variance models. The regularization parameter $\lambda$ determines the degree of regularization to apply and is typically determined through cross validation.
Ridge Regression¶
There are many forms for $\textbf{R}(\theta)$ but a common form is the squared $L^2$ norm of $\theta$.
$$\large \large \textbf{R}_{L^2}(\theta) = \large||\theta||_2^2 = \theta^T \theta = \sum_{k=1}^p \theta_k^2 $$
In the context of least squares regression this is often referred to as Ridge Regression with the objective:
$$ \large \hat{\theta} = \arg \min_\theta \frac{1}{n} \sum_{i=1}^n \left(y_i - f_\theta(x_i)\right)^2 + \lambda ||\theta||_2^2 $$
This is also sometimes called Tikhonov Regularization.
How does $L^2$ Regularization Help¶
The $L^2$ penalty helps in several ways:
Manages Model Complexity
- It ensures that uninformative features weights are relatively small (near zero) mitigating the affect of those features.
- It evenly distributes weight over similar features to reduce variance.
Practical Concerns
- It removes degeneracy created by co-linear features
- It improves the numerical stability of
Visualizing $L^2$ Regularization¶
In the following we visualize the regularization surface. Notice that it pushes weights towards zero but is relatively smooth around the origin.
theta_range = np.linspace(-2,2,100)
(u,v) = np.meshgrid(theta_range, theta_range)
w_values = np.vstack((u.flatten(), v.flatten())).T
def l2_sq_reg(w):
return np.sum(w**2)
reg_values = [l2_sq_reg(w) for w in w_values]
reg_surface = go.Surface(
x = u, y = v,
z = np.reshape(reg_values, u.shape),
contours=dict(z=dict(show=True))
)
# Axis labels
layout = go.Layout(
scene=go.Scene(
xaxis=go.XAxis(title='w0'),
yaxis=go.YAxis(title='w1'),
aspectratio=dict(x=2.,y=2., z=1.),
camera=dict(eye=dict(x=-2, y=-2, z=2))
)
)
fig = go.Figure(data = [reg_surface], layout = layout)
py.iplot(fig)
$L^1$ Regularization (Lasso)¶
Another common regularization function is the sum of the absolute values:
$$\large \large \textbf{R}_{L^1}(\theta) = \sum_{k=1}^p |\theta_k| $$
This is called $L^1$ regularization as it corresponds to the $L^1$ norm. Least squares linear regression in conjunction with the $L^1$ norm is often called the Lasso (Least Absolute Shrinkage and Selection Operator).
In contrast to the $L^2$ norm the $L^1$ norm encourages $\theta_i$ values to be exactly zero in less informative dimensions thereby reducing model complexity. To see how the $L^1$ encourages sparsity consider the following illustration:
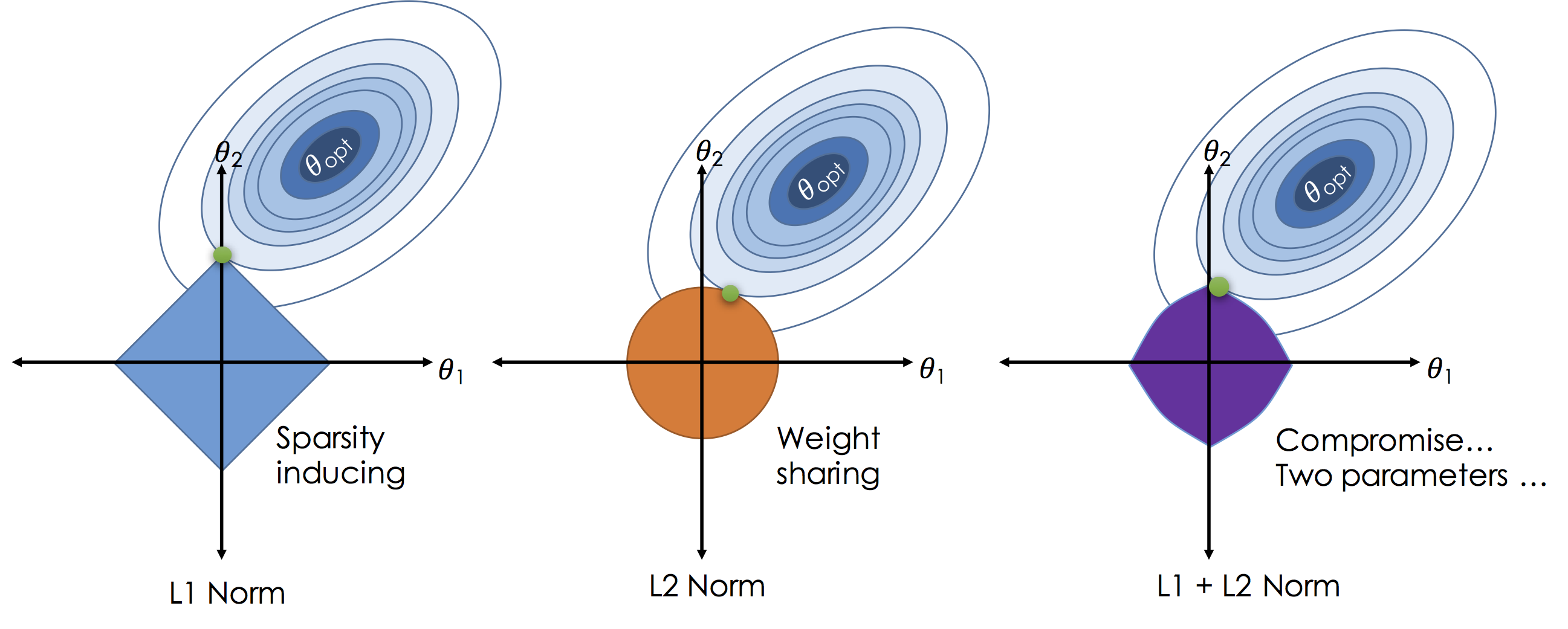
In the above figures we plot the loss for settings of a two dimensional ($\theta_1$ and $\theta_2$) model as the elliptical contours. Without regularization the solution would be at the center of the contours. By imposing regularization we constrain the solution to living in the "norm ball" centered at the origin (all zero theta vector). As we increase $\lambda$ we actually shrink the ball. Unlike the $L^2$ solutions in the $L^1$ will often "slide to the corners" which are aligned with axis causing subsets of the $\theta$ vector to be exactly zero.
In some settings a compromise can be achieved by using both the $L^2$ and $L^1$ norms to encourage sparsity while ensuring relatively co-linear features are given equal weight (to improve robustness).
theta_range = np.linspace(-2,2,100)
(u,v) = np.meshgrid(theta_range, theta_range)
w_values = np.vstack((u.flatten(), v.flatten())).T
def l1_reg(w):
return np.sum(np.abs(w))
reg_values = [l1_reg(w) for w in w_values]
reg_surface = go.Surface(
x = u, y = v,
z = np.reshape(reg_values, u.shape),
contours=dict(z=dict(show=True))
)
# Axis labels
layout = go.Layout(
scene=go.Scene(
xaxis=go.XAxis(title='w0'),
yaxis=go.YAxis(title='w1'),
aspectratio=dict(x=2.,y=2., z=1.),
camera=dict(eye=dict(x=-2, y=-2, z=2))
)
)
fig = go.Figure(data = [reg_surface], layout = layout)
py.iplot(fig)