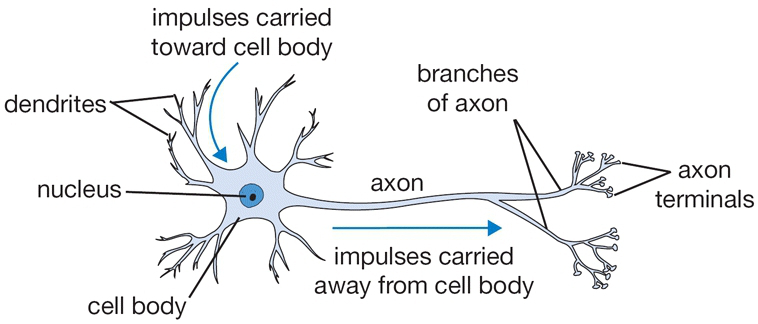
Neurons pass information from one to another using action potentials. They connect with one another at synapses, which are junctions between one neuron's axon and another's dendrite. Information flows from:
- The dendrites,
- To the cell body,
- Through the axons,
- To a synapse connecting the axon to the dendrite of the next neuron.
An Artificial Neuron is a mathematical function with the following elements:
- Input
- Weighted summation of inputs
- Processing unit of activation function
- Output
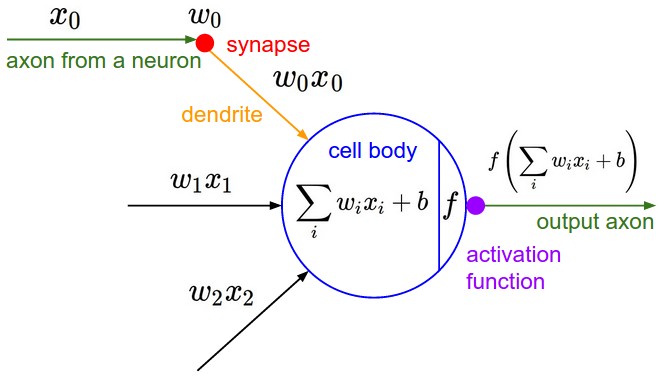
The mathematical equation for an artificial is as follows:
\begin{align} \hat{y} = f(\vec{\mathbf{\theta}} \cdot \vec{\mathbf{x}}) &= f(\sum_{i=0}^d \theta_i x_i) \\ &= f(\theta_0 + \theta_1 x_1 + ... + \theta_dx_d). \end{align}
Assuming that function $f$ is the logistic or sigmoid function, the output of the neuron has a probability value ($0 \leq p \leq 1$). This probability value can then be used for a binary classification task where $p < 0.5$ is an indication of class $0$, and $p \geq 0.5$ assigns data to class 1. Re-writing the equation above with a sigmoid activation function would give us the following:
\begin{align} \hat{y} = σ(\vec{\mathbf{\theta}} \cdot \vec{\mathbf{x}}) &= σ(\sum_{i=0}^d \theta_i x_i) \\ &= σ(\theta_0 + \theta_1 x_1 + ... + \theta_dx_d). \end{align}
The code below contains an implementation of AND, OR, and XOR gates. You will be able to generate data for each of the functions and add the desired noise level to the data. Familiarize yourself with the code and answer the following questions.
Creating the toy dataset¶
We'll start by generating synthetic data for a logic gate (e.g., AND, OR, XOR) with Gaussian noise. This data will be used for training and testing the logistic regression model.
The function generate_data_with_noise allows customization of the number of samples, the logic gate, and the noise level.
import numpy as np
import pandas as pd
# Function to generate a dataset with multiple samples per gate location
def generate_data_with_noise(num_samples = 500, gate = "AND", noise_level = 0.05):
"""
Generate multiple samples per logic gate configuration with added noise.
"""
if gate == 'AND':
base_X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
base_y = np.array([0, 0, 0, 1])
elif gate == 'OR':
base_X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
base_y = np.array([0, 1, 1, 1])
elif gate == 'XOR':
base_X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
base_y = np.array([0, 1, 1, 0])
else:
raise ValueError("Gate must be 'AND', 'OR', or 'XOR'.")
# Repeat each base configuration to create multiple samples
X = np.repeat(base_X, num_samples // len(base_X), axis=0)
y = np.repeat(base_y, num_samples // len(base_y), axis=0)
# Add Gaussian noise to the inputs
X = X + np.random.normal(0, noise_level, X.shape)
# Shuffle the dataset to avoid ordered samples
indices = np.arange(X.shape[0])
np.random.shuffle(indices)
X = X[indices]
y = y[indices]
return X, y
In this lecture we will use interactive visualizations. These require a python environment so if you are viewing this notebook through the static HTML version you won't be able to use the interactive features.
from ipywidgets import interact, FloatSlider, Dropdown, Checkbox
import plotly.express as px
import plotly.graph_objects as go
X, y = generate_data_with_noise(500, 'AND', 0.05)
# Make an interactive plot
data_fig = go.FigureWidget()
data_fig.add_trace(go.Scatter(x=X[y == 0, 0], y=X[y == 0, 1], mode='markers', marker=dict(color='red'), name='0'))
data_fig.add_trace(go.Scatter(x=X[y == 1, 0], y=X[y == 1, 1], mode='markers', marker=dict(color='blue'), name='1'))
data_fig.update_layout(width=800, height=500,
xaxis_range=[-1, 2], yaxis_range=[-1, 2])
# The following code defines a set of interactive widgets (sliders)
# and binds them to an update function that will be run whenever
# a slider is changed.
@interact(num_samples=FloatSlider(min=100, max=1000, step=100, value=500, description='Samples'),
gate=Dropdown(options=['AND', 'OR', 'XOR'], value='AND', description='Gate'),
noise_level=FloatSlider(min=0.0, max=1.0, step=0.01, value=0.05, description='Noise Level'))
def update_data_plot(num_samples, gate, noise_level):
X, y = generate_data_with_noise(num_samples, gate, noise_level)
with data_fig.batch_update():
data_fig.data[0].x = X[y == 0, 0]
data_fig.data[0].y = X[y == 0, 1]
data_fig.data[1].x = X[y == 1, 0]
data_fig.data[1].y = X[y == 1, 1]
data_fig.update_layout(title=f"Dataset for {gate} Gate with Noise Level {noise_level}")
data_fig
interactive(children=(FloatSlider(value=500.0, description='Samples', max=1000.0, min=100.0, step=100.0), Drop…
FigureWidget({
'data': [{'marker': {'color': 'red'},
'mode': 'markers',
'name': '0',
'type': 'scatter',
'uid': '0b9744c5-3d28-4ea6-b251-7829bd74736e',
'x': array([ 0.03250149, 0.01830668, -0.05692431, ..., -0.15004324, 0.07860124,
0.03399897]),
'y': array([ 1.00093641, 0.94820927, 0.97140887, ..., 0.07575058, -0.00405588,
-0.0175853 ])},
{'marker': {'color': 'blue'},
'mode': 'markers',
'name': '1',
'type': 'scatter',
'uid': 'c45e78ae-90a0-4267-8b1f-e0025c74bd5d',
'x': array([0.98813952, 0.92049489, 0.97406054, 1.01440182, 0.98185308, 1.0113955 ,
1.02575418, 0.91457084, 0.91427198, 1.07061732, 0.9405913 , 1.05711115,
1.01023693, 0.95124406, 0.94780585, 1.00560696, 1.02100218, 1.09926252,
0.95658512, 1.00291549, 0.88093311, 1.05410266, 1.07803598, 1.01144518,
0.97537758, 1.09112492, 0.9885781 , 0.99782944, 0.96493641, 0.96180292,
0.94908711, 0.91314409, 1.02959156, 0.998522 , 0.96494042, 0.90071902,
1.05488583, 1.02422931, 0.97135131, 1.00611015, 1.02188796, 0.98404889,
1.03760807, 1.06632959, 1.00789523, 1.04736195, 0.90770299, 1.04695235,
1.01712573, 0.88750124, 1.02528001, 0.95874563, 0.98174769, 1.03299362,
1.00270216, 1.01431431, 1.09924591, 0.97381269, 0.99073976, 1.0662258 ,
0.9958022 , 1.00593827, 1.07883489, 0.96394329, 1.01284866, 1.06124336,
0.97342523, 1.08193591, 1.04826273, 0.95422049, 1.00128834, 0.9100067 ,
1.04611785, 1.11585639, 0.99705428, 1.01840144, 1.04502955, 0.99152729,
0.95724416, 0.97137631, 0.98007543, 1.01882004, 0.98157186, 0.91381809,
0.97250143, 0.9776878 , 1.03126018, 1.00835072, 0.94840168, 1.0881151 ,
1.05033283, 0.99479352, 1.02205423, 1.03835352, 0.91626814, 1.02496384,
1.01012149, 0.96948828, 0.90323253, 0.99846926, 0.97560216, 0.90903044,
0.96848096, 0.97365348, 0.87417723, 0.99124655, 0.96351457, 1.03230015,
0.97807236, 1.02538813, 1.0247298 , 0.99307862, 0.92012788, 0.99332986,
1.06953258, 1.00766309, 1.09165622, 1.02457208, 1.03877328, 1.03635239,
0.96628472, 0.99822189, 1.02489548, 1.03377237, 1.05323428]),
'y': array([0.83019861, 1.00083931, 1.0039859 , 0.96134297, 0.99558773, 0.96597354,
0.99776127, 1.00045753, 0.95939304, 1.01842736, 1.00363966, 0.91445666,
0.96985144, 1.04224371, 0.91308662, 0.96265587, 1.03244751, 0.94303196,
1.02401113, 1.09883593, 0.98687421, 1.07431817, 0.92277544, 1.00582678,
1.05769078, 1.08965857, 0.96344417, 0.94083223, 0.99352731, 0.974481 ,
1.08912622, 0.9689995 , 0.96005317, 1.04571659, 1.03670195, 0.9487771 ,
0.94101971, 1.05698489, 1.01208531, 0.94853829, 1.07123548, 0.99217766,
1.07726772, 1.05156901, 1.05557511, 0.95299775, 1.01479284, 0.97548311,
0.97370457, 0.99208363, 1.03831786, 0.9606021 , 1.00540947, 1.00442152,
1.05821907, 0.90082126, 0.95286098, 0.93428732, 0.98784296, 1.01617919,
0.98175775, 1.04689661, 0.99958884, 0.97878682, 1.03898353, 1.05064367,
0.9577668 , 1.05525476, 1.06060027, 0.89803765, 1.00729917, 0.9520738 ,
0.99238571, 1.02594328, 0.93211913, 0.98761603, 1.00573536, 0.95055065,
0.97915037, 1.0424473 , 1.05666875, 1.01848044, 1.03597251, 1.00517152,
0.97898473, 0.99465496, 1.01284812, 0.99539868, 1.10224498, 0.99443273,
0.98424946, 0.97413256, 0.98951422, 0.91031639, 0.97091571, 0.95724796,
0.97672795, 1.03408661, 1.00170001, 0.95661331, 1.01990605, 0.98637752,
1.08765258, 0.94038376, 1.01263775, 1.01614272, 1.05269555, 1.00675051,
0.95834083, 1.04598932, 1.05462345, 0.9880109 , 1.06412548, 1.08845522,
0.96465331, 1.01056492, 0.93496895, 1.0004379 , 0.98887222, 1.02605057,
1.00151701, 1.0166722 , 0.96855967, 1.03095019, 0.965316 ])}],
'layout': {'height': 500,
'template': '...',
'title': {'text': 'Dataset for AND Gate with Noise Level 0.05'},
'width': 800,
'xaxis': {'range': [-1, 2]},
'yaxis': {'range': [-1, 2]}}
})
Logistic Regression Using Scikit-learn¶
This section demonstrates how to perform logistic regression using the scikit-learn library. The dataset is divided into training and testing subsets using an 80%-20% ratio with the train_test_split function. A logistic regression model is instantiated and trained on the training dataset using the .fit() method. The model's performance is evaluated on both the training and testing data using the .score() method, which computes accuracy.
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
# Logistic Regression Using Scikit-learn
def perform_logistic_regression(X, y):
# Split the data
x_train, x_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=140)
# Train a logistic regression model
model = LogisticRegression().fit(x_train, y_train)
# Print training and testing scores
train_error = model.score(x_train, y_train)
test_error = model.score(x_test, y_test)
return model, train_error, test_error
We can plot a decision boundary or even a decision surface by plotting predictions on a regular grid of points. This is accomplished using the meshgrid function from numpy. We can then use the model to predict the class of each point on the grid and plot the results. This is a useful way to visualize the decision boundary of a classifier.
def plot_decision_boundary(model, xrange, yrange, num_points=100, probs=True):
# Generate a grid of points
xx, yy = np.meshgrid(np.linspace(xrange[0], xrange[1], num_points),
np.linspace(yrange[0], yrange[1], num_points))
grid = np.c_[xx.ravel(), yy.ravel()]
# Get predictions for the grid
if probs:
preds = model.predict_proba(grid)[:,1].reshape(xx.shape)
else:
preds = model.predict(grid).reshape(xx.shape)
return go.Contour(x=xx[0], y=yy[:, 0], z=preds, colorscale=[[0, 'red'], [1, 'blue']],
opacity = 0.5, showscale=False)
Again we create an interactive visualization plot:
pred_fig = go.FigureWidget(data=data_fig.data, layout=data_fig.layout)
model, train_test, test_error = perform_logistic_regression(X, y)
boundary = plot_decision_boundary(model, [-1, 2], [-1, 2], probs=False)
pred_fig.add_trace(boundary)
@interact(num_samples=FloatSlider(min=100, max=1000, step=100, value=500, description='Samples'),
gate=Dropdown(options=['AND', 'OR', 'XOR'], value='AND', description='Gate'),
noise_level=FloatSlider(min=0.0, max=1.0, step=0.01, value=0.05, description='Noise Level'),
show_probs=Checkbox(value=False, description='Show Probabilities'))
def update_pred_fig(num_samples, gate, noise_level, show_probs):
np.random.seed(42)
X, y = generate_data_with_noise(num_samples, gate, noise_level)
model, train_error, test_error = perform_logistic_regression(X, y)
with pred_fig.batch_update():
pred_fig.data[0].x = X[y == 0, 0]
pred_fig.data[0].y = X[y == 0, 1]
pred_fig.data[1].x = X[y == 1, 0]
pred_fig.data[1].y = X[y == 1, 1]
pred_fig.data[2].z = plot_decision_boundary(model, [-1, 2], [-1, 2], probs=show_probs).z
pred_fig.update_layout(title=f"Predictions for {gate} Gate with Noise Level {noise_level} (Train: {train_error:.2f}, Test: {test_error:.2f})")
pred_fig
interactive(children=(FloatSlider(value=500.0, description='Samples', max=1000.0, min=100.0, step=100.0), Drop…
FigureWidget({
'data': [{'marker': {'color': 'red'},
'mode': 'markers',
'name': '0',
'type': 'scatter',
'uid': '983af166-8c61-49d1-9721-bc533847cef6',
'x': array([ 0.97386385, -0.03232864, -0.03008533, ..., 0.98181939, 0.91106399,
0.96942411]),
'y': array([ 0.05245046, 0.9459226 , 0.09261391, ..., -0.00284728, 0.07480222,
-0.07033305])},
{'marker': {'color': 'blue'},
'mode': 'markers',
'name': '1',
'type': 'scatter',
'uid': 'f436aa5b-7507-4c2f-9d53-98100565e7cc',
'x': array([0.96364314, 0.97224002, 0.94893836, 1.0246659 , 0.97411944, 1.03409457,
1.02798952, 0.93598478, 0.97767832, 1.01445843, 0.99065642, 1.00141592,
1.01335251, 1.00955495, 1.04691419, 1.07737526, 0.96936057, 0.96865165,
0.9916441 , 1.05333373, 1.05975233, 1.01429327, 0.97899066, 0.95383834,
1.07752502, 1.07234889, 0.97827519, 1.05368159, 0.968113 , 1.0782762 ,
0.97413558, 0.97769083, 0.97238885, 1.08988433, 0.99115264, 1.03251006,
0.99826576, 0.96618038, 1.02919641, 1.02200072, 0.99825058, 1.00143724,
0.97552803, 1.02953274, 1.03213614, 0.99834365, 0.97121811, 0.9275993 ,
0.99981987, 1.01014615, 0.97144105, 0.94594717, 1.00664848, 1.03929001,
1.01713627, 0.99917886, 1.0353876 , 0.95708211, 1.02148091, 1.07897861,
0.99802224, 1.03292721, 1.04102411, 1.03162039, 0.97772487, 0.93103404,
0.97738468, 1.05159223, 1.06910795, 1.04169611, 0.95120634, 1.02848836,
1.04203218, 0.98895179, 0.93200719, 0.96813064, 0.9438639 , 1.12634662,
0.95253006, 1.06278781, 0.98764113, 0.92372374, 1.04921612, 0.95838222,
1.00640522, 0.99551322, 1.00982606, 0.94979296, 0.99752681, 1.07516992,
0.99649171, 0.99523522, 1.01219004, 0.9977207 , 0.9879382 , 0.9979921 ,
0.97205391, 1.01246918, 1.03227421, 0.96884297, 1.00832261, 0.92080486,
1.12800423, 1.01110669, 0.949919 , 1.00888505, 1.06032545, 1.11494491,
1.00480604, 1.01900989, 1.01357894, 0.98461109, 1.09233185, 1.0041142 ,
0.95165119, 1.0310905 , 0.93742303, 1.01041914, 1.05746367, 0.99589244,
0.93277747, 0.99627833, 1.01843367, 1.03039483, 1.07102521]),
'y': array([0.98762407, 1.09405785, 1.03541782, 1.00924181, 1.0111894 , 1.09233537,
1.05403904, 1.04362287, 1.0097045 , 1.12276501, 0.97801345, 1.00148781,
1.04448154, 1.00232183, 0.97419776, 1.08979388, 0.98061492, 1.09062243,
1.00733568, 1.05846478, 0.92384065, 1.01672284, 0.98591077, 0.93241577,
0.9500823 , 1.00982774, 0.98454139, 0.94867424, 0.97345015, 0.99671249,
1.07046737, 0.90552296, 1.03164659, 1.03204214, 0.96008514, 0.99504121,
1.01171074, 1.09004702, 0.9820354 , 0.97489729, 1.08854003, 1.06392259,
1.05220804, 1.05543518, 1.06645763, 1.08972789, 1.00610049, 0.8900597 ,
0.94208177, 0.92421279, 1.02862914, 1.05265764, 0.96499396, 1.02127288,
1.02283766, 1.05941966, 0.97187666, 1.03501549, 1.01038438, 0.973857 ,
1.03407503, 1.10051023, 1.0253637 , 1.04862772, 1.07266922, 0.9634535 ,
0.87880603, 0.92572198, 1.03243549, 1.022959 , 1.05268209, 1.02238543,
0.9673688 , 1.00134429, 1.03731268, 1.05945083, 1.01912049, 0.97345656,
1.1316191 , 0.95526963, 0.96590079, 0.9654046 , 0.98930056, 1.02357078,
0.96594742, 1.07200586, 1.03545019, 0.96161012, 1.03374097, 1.04386811,
0.91695195, 1.01395108, 0.97179607, 1.01216697, 1.01760277, 0.92846124,
1.01886059, 1.07887266, 1.10816274, 0.97222614, 1.02462256, 1.03802073,
0.99519701, 0.97606257, 0.98594499, 0.93323278, 0.95915322, 0.98185807,
0.97688624, 1.03052929, 0.93616257, 1.01095752, 0.94649576, 1.05327402,
0.99761443, 0.92148876, 1.07218823, 0.89791326, 0.96484118, 1.05586479,
0.9540674 , 1.0310336 , 0.98033306, 1.00933046, 0.97146269])},
{'colorscale': [[0, 'red'], [1, 'blue']],
'opacity': 0.5,
'showscale': False,
'type': 'contour',
'uid': '0624df77-9108-4dad-a403-4091f3261f8a',
'x': array([-1. , -0.96969697, -0.93939394, -0.90909091, -0.87878788,
-0.84848485, -0.81818182, -0.78787879, -0.75757576, -0.72727273,
-0.6969697 , -0.66666667, -0.63636364, -0.60606061, -0.57575758,
-0.54545455, -0.51515152, -0.48484848, -0.45454545, -0.42424242,
-0.39393939, -0.36363636, -0.33333333, -0.3030303 , -0.27272727,
-0.24242424, -0.21212121, -0.18181818, -0.15151515, -0.12121212,
-0.09090909, -0.06060606, -0.03030303, 0. , 0.03030303,
0.06060606, 0.09090909, 0.12121212, 0.15151515, 0.18181818,
0.21212121, 0.24242424, 0.27272727, 0.3030303 , 0.33333333,
0.36363636, 0.39393939, 0.42424242, 0.45454545, 0.48484848,
0.51515152, 0.54545455, 0.57575758, 0.60606061, 0.63636364,
0.66666667, 0.6969697 , 0.72727273, 0.75757576, 0.78787879,
0.81818182, 0.84848485, 0.87878788, 0.90909091, 0.93939394,
0.96969697, 1. , 1.03030303, 1.06060606, 1.09090909,
1.12121212, 1.15151515, 1.18181818, 1.21212121, 1.24242424,
1.27272727, 1.3030303 , 1.33333333, 1.36363636, 1.39393939,
1.42424242, 1.45454545, 1.48484848, 1.51515152, 1.54545455,
1.57575758, 1.60606061, 1.63636364, 1.66666667, 1.6969697 ,
1.72727273, 1.75757576, 1.78787879, 1.81818182, 1.84848485,
1.87878788, 1.90909091, 1.93939394, 1.96969697, 2. ]),
'y': array([-1. , -0.96969697, -0.93939394, -0.90909091, -0.87878788,
-0.84848485, -0.81818182, -0.78787879, -0.75757576, -0.72727273,
-0.6969697 , -0.66666667, -0.63636364, -0.60606061, -0.57575758,
-0.54545455, -0.51515152, -0.48484848, -0.45454545, -0.42424242,
-0.39393939, -0.36363636, -0.33333333, -0.3030303 , -0.27272727,
-0.24242424, -0.21212121, -0.18181818, -0.15151515, -0.12121212,
-0.09090909, -0.06060606, -0.03030303, 0. , 0.03030303,
0.06060606, 0.09090909, 0.12121212, 0.15151515, 0.18181818,
0.21212121, 0.24242424, 0.27272727, 0.3030303 , 0.33333333,
0.36363636, 0.39393939, 0.42424242, 0.45454545, 0.48484848,
0.51515152, 0.54545455, 0.57575758, 0.60606061, 0.63636364,
0.66666667, 0.6969697 , 0.72727273, 0.75757576, 0.78787879,
0.81818182, 0.84848485, 0.87878788, 0.90909091, 0.93939394,
0.96969697, 1. , 1.03030303, 1.06060606, 1.09090909,
1.12121212, 1.15151515, 1.18181818, 1.21212121, 1.24242424,
1.27272727, 1.3030303 , 1.33333333, 1.36363636, 1.39393939,
1.42424242, 1.45454545, 1.48484848, 1.51515152, 1.54545455,
1.57575758, 1.60606061, 1.63636364, 1.66666667, 1.6969697 ,
1.72727273, 1.75757576, 1.78787879, 1.81818182, 1.84848485,
1.87878788, 1.90909091, 1.93939394, 1.96969697, 2. ]),
'z': array([[0, 0, 0, ..., 0, 0, 0],
[0, 0, 0, ..., 0, 0, 0],
[0, 0, 0, ..., 0, 0, 0],
...,
[0, 0, 0, ..., 1, 1, 1],
[0, 0, 0, ..., 1, 1, 1],
[0, 0, 0, ..., 1, 1, 1]])}],
'layout': {'height': 500,
'template': '...',
'title': {'text': 'Predictions for AND Gate with Noise Level 0.05 (Train: 1.00, Test: 1.00)'},
'width': 800,
'xaxis': {'range': [-1, 2]},
'yaxis': {'range': [-1, 2]}}
})
PyTorch¶
We can now try to repeat the modeling process using PyTorch. PyTorch is a popular deep learning library that is widely used in the research community. It is a lower-level library than scikit-learn and requires more code to accomplish the same tasks. However, it is more flexible and can be used to build more complex models.
# PyTorch
import torch
# Neural Network Class in pyTorch
import torch.nn as nn
# Optimizer Library in pyTorch (for SGD)
import torch.optim as optim
Step 0: Working with Data in Pytorch¶
At the core of PyTorch is the torch.Tensor class. This class is similar to numpy arrays but with some additional features. PyTorch tensors can be used to store data and perform operations on that data. Pytorch tensors can also be used to store gradients, which are used to update the parameters of a model during training.
To use PyTorch, we need to convert our data to tensors. We can do this using the torch.tensor function, or we can use the torch.from_numpy function to convert numpy arrays to tensors.
Notice that tensors are converted to type float32. This is because PyTorch is built around float32 instead of float64 (the standard format for numpy). This is because most of the math done on GPUs is in lower precision. The labels (y_train) are reshaped using .unsqueeze(1), which adds an additional dimension to match the model's expected output shape.
def make_tensors(X, y):
from torch.utils.data import random_split, TensorDataset
data = TensorDataset(torch.tensor(X, dtype=torch.float32),
torch.tensor(y, dtype=torch.float32).unsqueeze(1))
torch.manual_seed(140)
train_data, test_data = random_split(data, [0.8, 0.2])
return train_data, test_data
Step 1: Defining the Logistic Regression Model¶
The logistic regression model is implemented in PyTorch using the LogisticRegressionModel class, which inherits from nn.Module. In PyTorch, inheriting from nn.Module is essential, as it provides the necessary methods to manage layers and parameters within the model. In the __init__ method, a single linear layer is defined using nn.Linear(input_size, 1). This layer computes a weighted sum of the input features plus a bias term to form the mathematical basis of logistic regression. The input_size specifies the number of features in the dataset. In the forward method, the model performs the forward pass by applying the linear transformation followed by the sigmoid activation function (torch.sigmoid). The sigmoid activation ensures that the output values are in the range [0,1] so that the output is suitable for binary classification.
class LogisticRegressionModelA(nn.Module):
def __init__(self, input_size):
super().__init__()
self.intercept = nn.Parameter(torch.tensor(1.0))
self.w = nn.Parameter(torch.ones(input_size, 1))
def forward(self, x):
intercept = self.intercept
w = self.w
z = intercept + torch.matmul(x, w)
return torch.sigmoid(z)
class LogisticRegressionModelB(nn.Module):
def __init__(self, input_size):
super().__init__()
self.linear = nn.Linear(input_size, 1)
def forward(self, x):
return torch.sigmoid(self.linear(x))
model = LogisticRegressionModelB(2)
Step 2: Defining the Loss¶
Just as with the rest of Data100 and machine learning, we need to define a loss function. For logistic regression, we typically use the binary cross-entropy loss which is a special case of the more general Cross-Entropy Loss.
The loss function and optimizer are essential components for training a PyTorch model. In this implementation, the binary cross-entropy loss (nn.BCELoss) is used as the loss function. It measures the difference between the predicted probabilities and the true labels.
loss_fn = nn.BCELoss()
Step 3: Optimize the Loss¶
The optimizer used is stochastic gradient descent (optim.SGD). The optimizer updates the model's parameters during training to minimize the loss. It takes the model's parameters and the learning rate as inputs. We could actually try more advanced optimizers like Adam. Try uncommenting the Adam optimizer line.
The training process in PyTorch is handled within a loop that iterates over the dataset multiple epochs. For each epoch, we iterate over the training data in batches. For each batch, the following steps are performed:
- The gradients from the previous iteration are cleared using
optimizer.zero_grad(). - The forward pass is executed by passing the training data through the model, which computes predictions.
- The predictions are compared with the true labels using the loss function, and the loss is calculated.
- Backpropagation is performed using
loss.backward(), which computes the gradients of the loss with respect to the model’s parameters. - Finally, the optimizer updates the model’s parameters using these gradients through the
optimizer.step()method.
def perform_logistic_regression_pytorch(train_dataset,
test_dataset,
model, loss_fn,
batch_size=64,
nepochs=20):
from torch.utils.data import DataLoader
# Create a dataloader for training
train_loader = DataLoader(train_dataset, batch_size=batch_size, shuffle=True)
test_loader = DataLoader(test_dataset, batch_size=batch_size, shuffle=False)
# Define the optimizer (this is the update rule)
optimizer = optim.SGD(model.parameters(), lr=0.5)
# optimizer = optim.Adam(model.parameters(), lr=0.5)
for epoch in range(nepochs):
# Loop through all the batches
for batch, (X, y) in enumerate(train_loader):
# Zero the gradients to start the next step
optimizer.zero_grad()
# Compute prediction and loss
pred = model(X)
loss = loss_fn(pred, y)
# Backpropagation (compute the gradient)
loss.backward()
# Update the parameters using the optimizer's update rule
optimizer.step()
# Evaluate the model on the test data
# In practice, we often do this in batches too, since the data is too big to fit in memory
with torch.no_grad():
test_loss_sum = 0.0
for X_test, y_test in test_loader:
test_pred = model(X_test)
test_loss = loss_fn(test_pred, y_test)
test_loss_sum += test_loss.item()
num_test_batches = len(test_loader)
print(f"Epoch {epoch}, Loss: {loss.item()}, Test Loss: {test_loss_sum/num_test_batches}")
Let's run the optimizer!
train_dataset, test_dataset = make_tensors(X, y)
model = LogisticRegressionModelA(2)
perform_logistic_regression_pytorch(train_dataset, test_dataset, model, loss_fn)
Epoch 0, Loss: 0.6229490637779236, Test Loss: 0.551544725894928 Epoch 1, Loss: 0.549572229385376, Test Loss: 0.46463291347026825 Epoch 2, Loss: 0.4472154676914215, Test Loss: 0.4199940115213394 Epoch 3, Loss: 0.4101514220237732, Test Loss: 0.38414032757282257 Epoch 4, Loss: 0.3993256986141205, Test Loss: 0.3564014285802841 Epoch 5, Loss: 0.34731197357177734, Test Loss: 0.3294874280691147 Epoch 6, Loss: 0.27998536825180054, Test Loss: 0.3099343776702881 Epoch 7, Loss: 0.25412875413894653, Test Loss: 0.2927774488925934 Epoch 8, Loss: 0.2489190548658371, Test Loss: 0.2768632471561432 Epoch 9, Loss: 0.23951081931591034, Test Loss: 0.2623734176158905 Epoch 10, Loss: 0.24455997347831726, Test Loss: 0.2536010518670082 Epoch 11, Loss: 0.2500861883163452, Test Loss: 0.23901592940092087 Epoch 12, Loss: 0.218313530087471, Test Loss: 0.22828186303377151 Epoch 13, Loss: 0.23970897495746613, Test Loss: 0.21750976890325546 Epoch 14, Loss: 0.30330318212509155, Test Loss: 0.20764698833227158 Epoch 15, Loss: 0.21686653792858124, Test Loss: 0.20029331743717194 Epoch 16, Loss: 0.21423457562923431, Test Loss: 0.19443674385547638 Epoch 17, Loss: 0.22573214769363403, Test Loss: 0.18666155636310577 Epoch 18, Loss: 0.16270937025547028, Test Loss: 0.18061764538288116 Epoch 19, Loss: 0.1728993058204651, Test Loss: 0.17477348446846008
Step 4: Crazy Interactive Visualization¶
After training, the decision boundary of the logistic regression model is visualized. A grid of points covering the feature space is created using np.mgrid. These grid points are passed through the trained model to predict probabilities. The predictions are reshaped into a format suitable for contour plotting.
The train_and_visualize_pytorch function integrates the PyTorch logistic regression implementation with an interactive widget. The function dynamically updates the dataset and decision boundary based on the selected logic gate (AND, OR, XOR) and noise_level.
def plot_decision_boundary_pytorch(model, xrange, yrange, num_points=100, probs=True):
# Generate a grid of points
xx, yy = torch.meshgrid(torch.linspace(xrange[0], xrange[1], num_points),
torch.linspace(yrange[0], yrange[1], num_points),
indexing='ij')
grid = torch.cat([xx.reshape(-1, 1), yy.reshape(-1, 1)], dim=1)
with torch.no_grad():
# Get predictions for the grid
if probs:
preds = model(grid).reshape(xx.shape)
else:
preds = (model(grid) > 0.5).float().reshape(xx.shape)
return go.Contour(x=xx[:, 0], y=yy[0], z=preds, colorscale=[[0, 'red'], [1, 'blue']],
opacity = 0.5, showscale=False)
# Interactive Widget for Decision Boundary Visualization
pred_fig = go.FigureWidget(data=data_fig.data, layout=data_fig.layout)
model_type = LogisticRegressionModelA
train_dataset, test_dataset = make_tensors(X, y)
model = model_type(2)
perform_logistic_regression_pytorch(train_dataset, test_dataset, model, loss_fn)
boundary = plot_decision_boundary_pytorch(model, [-1, 2], [-1, 2], probs=False)
pred_fig.add_trace(boundary)
display(pred_fig)
@interact(num_samples=FloatSlider(min=100, max=1000, step=100, value=500, description='Samples'),
gate=Dropdown(options=['AND', 'OR', 'XOR'], value='AND', description='Gate'),
noise_level=FloatSlider(min=0.0, max=1.0, step=0.01, value=0.05, description='Noise Level'),
show_probs=Checkbox(value=False, description='Show Probabilities'))
def update_pred_fig(num_samples, gate, noise_level, show_probs):
np.random.seed(42)
X, y = generate_data_with_noise(num_samples, gate, noise_level)
train_dataset, test_dataset = make_tensors(X, y)
model = model_type(2)
perform_logistic_regression_pytorch(train_dataset, test_dataset, model, loss_fn)
boundary = plot_decision_boundary_pytorch(model, [-1, 2], [-1, 2], probs=show_probs)
with pred_fig.batch_update():
pred_fig.data[0].x = X[y == 0, 0]
pred_fig.data[0].y = X[y == 0, 1]
pred_fig.data[1].x = X[y == 1, 0]
pred_fig.data[1].y = X[y == 1, 1]
pred_fig.data[2].z = boundary.z
Epoch 0, Loss: 0.6229490637779236, Test Loss: 0.551544725894928 Epoch 1, Loss: 0.549572229385376, Test Loss: 0.46463291347026825 Epoch 2, Loss: 0.4472154676914215, Test Loss: 0.4199940115213394 Epoch 3, Loss: 0.4101514220237732, Test Loss: 0.38414032757282257 Epoch 4, Loss: 0.3993256986141205, Test Loss: 0.3564014285802841 Epoch 5, Loss: 0.34731197357177734, Test Loss: 0.3294874280691147 Epoch 6, Loss: 0.27998536825180054, Test Loss: 0.3099343776702881 Epoch 7, Loss: 0.25412875413894653, Test Loss: 0.2927774488925934 Epoch 8, Loss: 0.2489190548658371, Test Loss: 0.2768632471561432 Epoch 9, Loss: 0.23951081931591034, Test Loss: 0.2623734176158905 Epoch 10, Loss: 0.24455997347831726, Test Loss: 0.2536010518670082 Epoch 11, Loss: 0.2500861883163452, Test Loss: 0.23901592940092087 Epoch 12, Loss: 0.218313530087471, Test Loss: 0.22828186303377151 Epoch 13, Loss: 0.23970897495746613, Test Loss: 0.21750976890325546 Epoch 14, Loss: 0.30330318212509155, Test Loss: 0.20764698833227158 Epoch 15, Loss: 0.21686653792858124, Test Loss: 0.20029331743717194 Epoch 16, Loss: 0.21423457562923431, Test Loss: 0.19443674385547638 Epoch 17, Loss: 0.22573214769363403, Test Loss: 0.18666155636310577 Epoch 18, Loss: 0.16270937025547028, Test Loss: 0.18061764538288116 Epoch 19, Loss: 0.1728993058204651, Test Loss: 0.17477348446846008
FigureWidget({
'data': [{'marker': {'color': 'red'},
'mode': 'markers',
'name': '0',
'type': 'scatter',
'uid': '74a487bc-c745-4e8d-a4cf-3f26b60d881f',
'x': array([ 0.03250149, 0.01830668, -0.05692431, ..., -0.15004324, 0.07860124,
0.03399897]),
'y': array([ 1.00093641, 0.94820927, 0.97140887, ..., 0.07575058, -0.00405588,
-0.0175853 ])},
{'marker': {'color': 'blue'},
'mode': 'markers',
'name': '1',
'type': 'scatter',
'uid': '8444aba5-9730-4655-8339-04406115bb8f',
'x': array([0.98813952, 0.92049489, 0.97406054, 1.01440182, 0.98185308, 1.0113955 ,
1.02575418, 0.91457084, 0.91427198, 1.07061732, 0.9405913 , 1.05711115,
1.01023693, 0.95124406, 0.94780585, 1.00560696, 1.02100218, 1.09926252,
0.95658512, 1.00291549, 0.88093311, 1.05410266, 1.07803598, 1.01144518,
0.97537758, 1.09112492, 0.9885781 , 0.99782944, 0.96493641, 0.96180292,
0.94908711, 0.91314409, 1.02959156, 0.998522 , 0.96494042, 0.90071902,
1.05488583, 1.02422931, 0.97135131, 1.00611015, 1.02188796, 0.98404889,
1.03760807, 1.06632959, 1.00789523, 1.04736195, 0.90770299, 1.04695235,
1.01712573, 0.88750124, 1.02528001, 0.95874563, 0.98174769, 1.03299362,
1.00270216, 1.01431431, 1.09924591, 0.97381269, 0.99073976, 1.0662258 ,
0.9958022 , 1.00593827, 1.07883489, 0.96394329, 1.01284866, 1.06124336,
0.97342523, 1.08193591, 1.04826273, 0.95422049, 1.00128834, 0.9100067 ,
1.04611785, 1.11585639, 0.99705428, 1.01840144, 1.04502955, 0.99152729,
0.95724416, 0.97137631, 0.98007543, 1.01882004, 0.98157186, 0.91381809,
0.97250143, 0.9776878 , 1.03126018, 1.00835072, 0.94840168, 1.0881151 ,
1.05033283, 0.99479352, 1.02205423, 1.03835352, 0.91626814, 1.02496384,
1.01012149, 0.96948828, 0.90323253, 0.99846926, 0.97560216, 0.90903044,
0.96848096, 0.97365348, 0.87417723, 0.99124655, 0.96351457, 1.03230015,
0.97807236, 1.02538813, 1.0247298 , 0.99307862, 0.92012788, 0.99332986,
1.06953258, 1.00766309, 1.09165622, 1.02457208, 1.03877328, 1.03635239,
0.96628472, 0.99822189, 1.02489548, 1.03377237, 1.05323428]),
'y': array([0.83019861, 1.00083931, 1.0039859 , 0.96134297, 0.99558773, 0.96597354,
0.99776127, 1.00045753, 0.95939304, 1.01842736, 1.00363966, 0.91445666,
0.96985144, 1.04224371, 0.91308662, 0.96265587, 1.03244751, 0.94303196,
1.02401113, 1.09883593, 0.98687421, 1.07431817, 0.92277544, 1.00582678,
1.05769078, 1.08965857, 0.96344417, 0.94083223, 0.99352731, 0.974481 ,
1.08912622, 0.9689995 , 0.96005317, 1.04571659, 1.03670195, 0.9487771 ,
0.94101971, 1.05698489, 1.01208531, 0.94853829, 1.07123548, 0.99217766,
1.07726772, 1.05156901, 1.05557511, 0.95299775, 1.01479284, 0.97548311,
0.97370457, 0.99208363, 1.03831786, 0.9606021 , 1.00540947, 1.00442152,
1.05821907, 0.90082126, 0.95286098, 0.93428732, 0.98784296, 1.01617919,
0.98175775, 1.04689661, 0.99958884, 0.97878682, 1.03898353, 1.05064367,
0.9577668 , 1.05525476, 1.06060027, 0.89803765, 1.00729917, 0.9520738 ,
0.99238571, 1.02594328, 0.93211913, 0.98761603, 1.00573536, 0.95055065,
0.97915037, 1.0424473 , 1.05666875, 1.01848044, 1.03597251, 1.00517152,
0.97898473, 0.99465496, 1.01284812, 0.99539868, 1.10224498, 0.99443273,
0.98424946, 0.97413256, 0.98951422, 0.91031639, 0.97091571, 0.95724796,
0.97672795, 1.03408661, 1.00170001, 0.95661331, 1.01990605, 0.98637752,
1.08765258, 0.94038376, 1.01263775, 1.01614272, 1.05269555, 1.00675051,
0.95834083, 1.04598932, 1.05462345, 0.9880109 , 1.06412548, 1.08845522,
0.96465331, 1.01056492, 0.93496895, 1.0004379 , 0.98887222, 1.02605057,
1.00151701, 1.0166722 , 0.96855967, 1.03095019, 0.965316 ])},
{'colorscale': [[0, 'red'], [1, 'blue']],
'opacity': 0.5,
'showscale': False,
'type': 'contour',
'uid': '32d47d80-b327-48bf-9e1b-c123cf73a473',
'x': array([-1.00000000e+00, -9.69696999e-01, -9.39393938e-01, -9.09090877e-01,
-8.78787875e-01, -8.48484874e-01, -8.18181813e-01, -7.87878752e-01,
-7.57575750e-01, -7.27272749e-01, -6.96969688e-01, -6.66666627e-01,
-6.36363626e-01, -6.06060624e-01, -5.75757563e-01, -5.45454502e-01,
-5.15151501e-01, -4.84848469e-01, -4.54545438e-01, -4.24242407e-01,
-3.93939376e-01, -3.63636345e-01, -3.33333313e-01, -3.03030282e-01,
-2.72727251e-01, -2.42424220e-01, -2.12121189e-01, -1.81818157e-01,
-1.51515126e-01, -1.21212095e-01, -9.09090638e-02, -6.06060326e-02,
-3.03030014e-02, 2.98023224e-08, 3.03030610e-02, 6.06060922e-02,
9.09091234e-02, 1.21212155e-01, 1.51515186e-01, 1.81818217e-01,
2.12121248e-01, 2.42424279e-01, 2.72727311e-01, 3.03030342e-01,
3.33333373e-01, 3.63636404e-01, 3.93939435e-01, 4.24242467e-01,
4.54545498e-01, 4.84848529e-01, 5.15151501e-01, 5.45454502e-01,
5.75757504e-01, 6.06060565e-01, 6.36363626e-01, 6.66666627e-01,
6.96969628e-01, 7.27272689e-01, 7.57575750e-01, 7.87878752e-01,
8.18181753e-01, 8.48484814e-01, 8.78787875e-01, 9.09090877e-01,
9.39393878e-01, 9.69696939e-01, 1.00000000e+00, 1.03030300e+00,
1.06060600e+00, 1.09090900e+00, 1.12121212e+00, 1.15151513e+00,
1.18181813e+00, 1.21212125e+00, 1.24242425e+00, 1.27272725e+00,
1.30303025e+00, 1.33333325e+00, 1.36363637e+00, 1.39393938e+00,
1.42424238e+00, 1.45454550e+00, 1.48484850e+00, 1.51515150e+00,
1.54545450e+00, 1.57575750e+00, 1.60606062e+00, 1.63636363e+00,
1.66666663e+00, 1.69696975e+00, 1.72727275e+00, 1.75757575e+00,
1.78787875e+00, 1.81818175e+00, 1.84848487e+00, 1.87878788e+00,
1.90909088e+00, 1.93939400e+00, 1.96969700e+00, 2.00000000e+00],
dtype=float32),
'y': array([-1.00000000e+00, -9.69696999e-01, -9.39393938e-01, -9.09090877e-01,
-8.78787875e-01, -8.48484874e-01, -8.18181813e-01, -7.87878752e-01,
-7.57575750e-01, -7.27272749e-01, -6.96969688e-01, -6.66666627e-01,
-6.36363626e-01, -6.06060624e-01, -5.75757563e-01, -5.45454502e-01,
-5.15151501e-01, -4.84848469e-01, -4.54545438e-01, -4.24242407e-01,
-3.93939376e-01, -3.63636345e-01, -3.33333313e-01, -3.03030282e-01,
-2.72727251e-01, -2.42424220e-01, -2.12121189e-01, -1.81818157e-01,
-1.51515126e-01, -1.21212095e-01, -9.09090638e-02, -6.06060326e-02,
-3.03030014e-02, 2.98023224e-08, 3.03030610e-02, 6.06060922e-02,
9.09091234e-02, 1.21212155e-01, 1.51515186e-01, 1.81818217e-01,
2.12121248e-01, 2.42424279e-01, 2.72727311e-01, 3.03030342e-01,
3.33333373e-01, 3.63636404e-01, 3.93939435e-01, 4.24242467e-01,
4.54545498e-01, 4.84848529e-01, 5.15151501e-01, 5.45454502e-01,
5.75757504e-01, 6.06060565e-01, 6.36363626e-01, 6.66666627e-01,
6.96969628e-01, 7.27272689e-01, 7.57575750e-01, 7.87878752e-01,
8.18181753e-01, 8.48484814e-01, 8.78787875e-01, 9.09090877e-01,
9.39393878e-01, 9.69696939e-01, 1.00000000e+00, 1.03030300e+00,
1.06060600e+00, 1.09090900e+00, 1.12121212e+00, 1.15151513e+00,
1.18181813e+00, 1.21212125e+00, 1.24242425e+00, 1.27272725e+00,
1.30303025e+00, 1.33333325e+00, 1.36363637e+00, 1.39393938e+00,
1.42424238e+00, 1.45454550e+00, 1.48484850e+00, 1.51515150e+00,
1.54545450e+00, 1.57575750e+00, 1.60606062e+00, 1.63636363e+00,
1.66666663e+00, 1.69696975e+00, 1.72727275e+00, 1.75757575e+00,
1.78787875e+00, 1.81818175e+00, 1.84848487e+00, 1.87878788e+00,
1.90909088e+00, 1.93939400e+00, 1.96969700e+00, 2.00000000e+00],
dtype=float32),
'z': array([[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
...,
[0., 0., 0., ..., 1., 1., 1.],
[0., 0., 0., ..., 1., 1., 1.],
[0., 0., 0., ..., 1., 1., 1.]], dtype=float32)}],
'layout': {'height': 500,
'template': '...',
'title': {'text': 'Dataset for AND Gate with Noise Level 0.05'},
'width': 800,
'xaxis': {'range': [-1, 2]},
'yaxis': {'range': [-1, 2]}}
})
interactive(children=(FloatSlider(value=500.0, description='Samples', max=1000.0, min=100.0, step=100.0), Drop…